题目内容
【题目】正比例函数y1=mx（m＞0）的图象与反比例函数y2= 
（k≠0）的图象交于点A（n，4）和点B，AM⊥y轴，垂足为M．若△AMB的面积为8，则满足y1＞y2的实数x的取值范围是 ．
【答案】﹣2＜x＜0或x＞2
【解析】解：∵正比例函数y1=mx（m＞0）的图象与反比例函数y2= 
（k≠0）的图象交于点A（n，4）和点B， ∴B（﹣n，﹣4）．
∵△AMB的面积为8，
∴ 
×8×n=8，
解得n=2，
∴A（2，4），B（﹣2，﹣4）．
由图形可知，当﹣2＜x＜0或x＞2时，正比例函数y1=mx（m＞0）的图象在反比例函数y2= （k≠0）图象的上方，即y1＞y2 ．
故答案为﹣2＜x＜0或x＞2．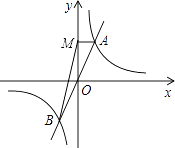
由反比例函数图象的对称性可得：点A和点B关于原点对称，再根据△AMB的面积为8列出方程 ×4n×2=8，解方程求出n的值，然后利用图象可知满足y1＞y2的实数x的取值范围．
练习册系列答案
相关题目
【题目】已知：二次函数y=ax2+bx+c（a≠0）中的x和y满足下表：
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | ﹣1 | 0 | m | 8 | … |
（1）可求得m的值为；
（2）求出这个二次函数的解析式；
（3）当y＞3时，x的取值范围为 ．
