题目内容
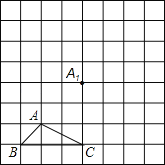
【题目】已知:等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.
(Ⅰ)若BP=QC,求证:AP=PQ;
(Ⅱ)若AP=PQ,求∠APQ的度数.


【答案】(1)见解析;(2)60°.
【解析】
(1)连接AQ,根据等边三角形的性质,得出AB=AC=BC,∠B=∠BAC=∠ACB=∠ACF= 60°,根据SAS求得△ABP≌△ACQ,得出AP=AQ,∠BAP=∠CAQ,可得出∠PAQ= 60°,则△PAQ是等边三角形,即可求得AP=PQ;
(2)在CF上截取CQ′=BP,根据等边三角形的性质,得出AB=AC=BC,∠B=∠ACB=60°,根据SAS求得△ABP≌△ACQ′,得出△PAQ′是等边三角形,从而证得Q′和Q是同一点,即可求得∠APQ=60°.
证明:(1)连接AQ,
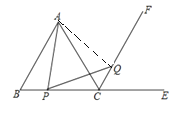
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠BAC=∠ACB = 60°,
∴∠ACE=120°,
∵CF平分∠ACE,
∴∠ACQ=60°=∠B,
在△ABP与△ACQ中,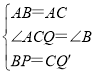
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ,
∴∠CAQ+∠PAC=∠BAP+∠PAC=60°
即∠PAQ=60°,
∴△PAQ是等边三角形,
∴AP=PQ;
(2)解:在CF上截取CQ′=BP,
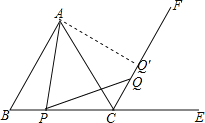
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠ACB=60°,
∴∠ACE=120°,
∵CF平分∠ACE,
∴∠ACQ=60°=∠B,
在△ABP与△ACQ′中,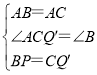
∴△ABP≌△ACQ′(SAS),
∴AP=AQ′,∠BAP=∠CAQ′,
∴∠CAQ′+∠PAC=∠BAP+∠PAC=60°
即∠PAQ′=60°,
∴△PAQ′是等边三角形,
∴AP=PQ′,∠APQ′=60°
∵AP=PQ,
∴PQ=PQ′,
∴Q′和Q是同一点,
∴∠APQ=60°.

【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?