题目内容
如图,∠B=∠D=Rt∠,AB=CD=b,BC=DE=a,AC=c,
(1)请问△ACE是否为等腰直角三角形?请说明理由.
(2)请你通过两种不同方法计算梯形ABDE的面积,并利用计算的结果验证勾股定理a2+b2=c2
(3)你能运用上面图形中若干个Rt△ABC构造出另一种证明勾股定理的图形吗?请画出构造后的示意图.(无需证明)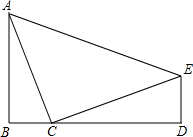
(1)请问△ACE是否为等腰直角三角形?请说明理由.
(2)请你通过两种不同方法计算梯形ABDE的面积,并利用计算的结果验证勾股定理a2+b2=c2
(3)你能运用上面图形中若干个Rt△ABC构造出另一种证明勾股定理的图形吗?请画出构造后的示意图.(无需证明)

(1)在Rt△ABC与Rt△CDE中,
∵
,
∴Rt△ABC≌Rt△CDE(SAS),
∴∠ACB=∠CED,AC=CE=c,
∵∠CED+∠ECD=90°,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∴△ACE是等腰直角三角形;
(2)∵S梯形=
(a+b)(a+b)=
(a+b)2,S梯形=2×
ab+
c2,
∴
(a+b)2=2×
ab+
c2,
整理得,a2+b2=c2;
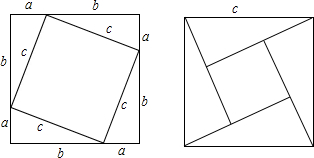
(3)如图所示,此题答案不唯一.
∵
|
∴Rt△ABC≌Rt△CDE(SAS),
∴∠ACB=∠CED,AC=CE=c,
∵∠CED+∠ECD=90°,

∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∴△ACE是等腰直角三角形;
(2)∵S梯形=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得,a2+b2=c2;
(3)如图所示,此题答案不唯一.

练习册系列答案
相关题目
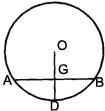 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

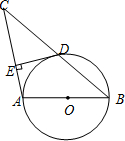 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.