题目内容
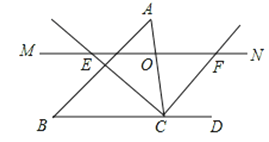
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.

(1)试说明:DG∥BC;
(2)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)∠3=71°.
【解析】
(1)由CD⊥AB,EF⊥AB即可得出CD//EF,从而得出∠2=∠BCD,再根据∠1=∠2即可得出∠1=∠BCD,依据“内错角相等,两直线平行”即可证出DG//BC;
(2)在Rt△BEF中,利用三角形内角和为180°即可算出∠2度数,从而得出∠BCD的度数,再根据BC//DG即可得出∠3=∠ACB,通过角的计算即可得出结论.
(1)证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴DG//BC;
(3) 解:在Rt△BEF中,
∵∠B=54°,
∴∠2=180°-90°-54°=36°,
又∵![]()
∴∠BCD=∠2=36°.
∵ ![]() ,
,
∴∠BCA=∠BCD + ∠ACD = 36°+ 35°= 71° .
又∵BC//DG,
∴∠3=∠BCA = 71°.

练习册系列答案
相关题目