Question

【题目】已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE＝OB，联结DE．

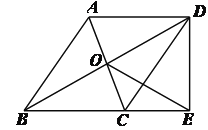
(1)求证：DE⊥BE；

(2)如果OE⊥CD，求证：BD CE＝CD DE．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

试题分析：（1）由平行四边形的性质得到BO=BD，由等量代换推出OE=BD，根据平行四边形的判定即可得到结论；

（2）根据等角的余角相等，得到∠CEO=∠CDE，推出△BDE∽△CDE，即可得到结论．

试题解析：（1）∵四边形ABCD是平行四边形，

∴BO=OD，

∵OE=OB，

∴OE=OD，

∴∠OBE=∠OEB，∠OED=∠ODE，

∵∠OBE+∠OEB+∠OED+∠ODE=180°，

∴∠BEO+∠DEO=∠BED=90°，

∴DE⊥BE；

（2）∵OE⊥CD

∴∠CEO+∠DCE=∠CDE+∠DCE=90°，

∴∠CEO=∠CDE，

∵OB=OE，

∴∠DBE=∠CDE，

∵∠BED=∠BED，

∴△BDE∽△DCE，

∴，

∴BD CE=CD DE．