题目内容
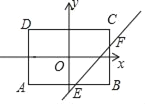
【题目】将含有45°角的直角三角板ABC和直尺如图摆放在桌子上,然后分别过A、B两个顶点向直尺作两条垂线段AD,BE.
(1)请写出图中的一对全等三角形并证明;
(2)你能发现并证明线段AD,BE,DE之间的关系吗?
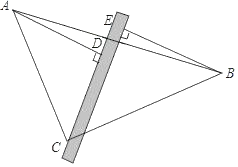
【答案】(1)△ADC≌△CEB(2)AD=BE+DE
【解析】
(1)结论:△ADC≌△CEB.根据AAS证明即可;
(2)由三角形全等的性质即可解决问题;
解:(1)结论:△ADC≌△CEB.
理由:∵AD⊥CE,BE⊥CE,
∴∠ACB=∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,∠ACD+∠ECB=90°,
∴∠CAD=∠ECB,
∵AC=CB,
∴△ADC≌△CEB(AAS).
(2)结论:AD=BE+DE.
理由:∵△ADC≌△CEB,
∴AD=CE,CD=BE,
∵CE=CD+DE,
∴AD=BE+DE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目