Question

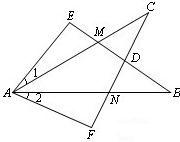19、如图．∠E=∠F=90°，∠B=∠C，AE=AF，请连接AD，并写出根据所给条件推出的三个正确结论

答案不唯一，如：AD平分∠EDF；△AEM≌△AFN；ED=DF；…写对一个得1分，最多得3分

．

Answer 1

分析：已知∠E=∠F=90°，∠B=∠C，AE=AF?∠EAB=∠FAC?△AEB≌△AFC；
∠1=∠2，AE=AF，∠E=∠F?△AEM≌△AFN（AAS）；
连接AD，由△AEM≌△AFN可得AM=AN，AD=AD，∠EDN=∠NDE?△AMD≌△AND?AD平分∠EDF．

解答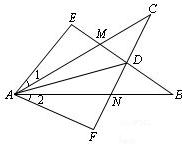：解：∵∠E=∠F=90°，∠B=∠C，AE=AF?∠EAB=∠FAC?△AEB≌△AFC①；
∵∠1=∠2，AE=AF，∠E=∠F?△AEM≌△AFN（AAS）②；
如图，连接AD，∵△AEM≌△AFN，
∴AM=AN，
而AD=AD，∠EDN=∠NDE，
∴△AMD≌△AND③，
∴AD平分∠EDF④．
故填空答案：AD平分∠EDF，△AEM≌△AFN，△AEB≌AFC等等．

点评：本题考查了三角形全等的判定与性质；答案可有多种．要求学生对于全等三角形的判定方法比较熟悉．