题目内容
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.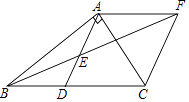
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
【答案】
(1)证明:如图,∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
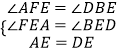 ,
,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵DB=DC,
∴AF=CD,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC= ![]() BC,
BC,
∴四边形ADCF是菱形;
(2)解:连接DF,
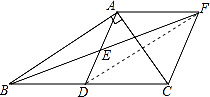
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S= ![]() ACDF=10.
ACDF=10.
【解析】(1)根据已知易证△AFE≌△DBE,得出AF=DB.根据D是BC的中点,得出DB=DC,从而证得AF=CD,可证得四边形ADCF是平行四边形,再根据直角三角形斜边上的中线等于斜边的一半,得出一组邻边相等,即AD=DC,即可证得结论。
(2)先证明四边形ABDF是平行四边形,得出DF的长,根据菱形的面积等于对角线之积的一半,即可求得结果。

练习册系列答案
相关题目



