题目内容
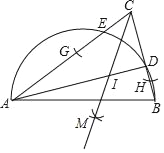
【题目】阅读下面材料：如图，AB是半圆的直径，点D、E在半圆上，且D为弧BE的中点，连接AE、BD并延长，交圆外一点C，按以下步骤作图：
①以点C为圆心，小于BC长为半径画弧，分别交AC、BC于点G、H；
②分别以点G、H为圆心，大于
GH的长为半径画弧，两弧相交于点M；
③作射线CM，交连接A、D两点的线段于点I．
则点I到△ABC各边的距离_____．（填“相等”或“不等”）
【答案】相等．
【解析】分析：根据角平分线的作图方法可知：CM是∠ACB的平分线，根据弧相等则圆心角相等，所对的圆周角相等可知：AD也是角平分线，所以I是角平分线的交点，根据角平分线的性质可得结论．
详解：根据作图过程可知：CM是∠ACB的平分线，
∵D是
的中点，
∴
，
∴∠CAD=∠BAD，
∴AD平分∠BAC，
∴I是△ABC角平分线的交点，
∴点I到△ABC各边的距离相等；
故答案为：相等．
练习册系列答案
相关题目
