题目内容
【题目】如图,长方形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4![]() ,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为( )
,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为( )

A.(6,4)B.(4,6)C.(-6,4)D.(-4,6)
【答案】A
【解析】
先求出C点坐标,根据OC点绕原点旋转,找出规律即可求解.
如图,过点C作CE⊥y轴于点E,连接OC,
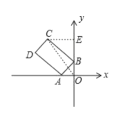
∵OA=OB=2
∴∠ABO=∠BAO=45°,
∵∠ABC=90°
∴∠CBE=45,
∵BC=AD=![]() ,
,
∴CE=BE=4,
∴OE=OB+BE=6,
∴C(-4,6),
∵矩形ABCD绕点O顺时针旋转,每次旋转90°,
则第1次旋转结束时,点C的坐标为(6,4);
第2次旋转结束时,点C的坐标为(4,-6);
则第3次旋转结束时,点C的坐标为(-6,-4);
则第4次旋转结束时,点C的坐标为(-4,6);
……
发现规律:旋转4次一个循环,
∴2021÷4=505…1,
则第2021次旋转结束时,点C的坐标为(6,4),
故选:A.

练习册系列答案
相关题目