题目内容
已知等腰三角形ABC内接于半径为5的⊙O中,如果底边BC的长为8,那么底角的正切值是 .
【答案】分析:作出圆的直径AE,则BD是直角△ABE斜边上的高线,理解利用射影定理求得AD的长,即可求解.
解答: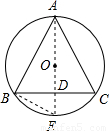 解:作出圆的直径AE,
解:作出圆的直径AE,
则∠ABE=90°,BC⊥AE,BD= BC=4.
BC=4.
∴BD2=AD•DE
设AD=x,则DE=10-x.
∴42=x(10-x)
解得:x=2或8.
∴tan∠ABD= 或
或
即tan∠ABD=2或 .
.
故答案为:2或 .
.
点评:本题主要考查了射影定理,垂径定理,正确求得AD的长是解题的关键.
解答:
 解:作出圆的直径AE,
解:作出圆的直径AE,则∠ABE=90°,BC⊥AE,BD=
 BC=4.
BC=4.∴BD2=AD•DE
设AD=x,则DE=10-x.
∴42=x(10-x)
解得:x=2或8.
∴tan∠ABD=
 或
或
即tan∠ABD=2或
 .
.故答案为:2或
 .
.点评:本题主要考查了射影定理,垂径定理,正确求得AD的长是解题的关键.

练习册系列答案
相关题目

 15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是
15、如图,已知等腰三角形ABC中,AC=BC,D为BC边上一点,且AB=AD,若不再添加辅助线,图中与∠C相等的角是 如图,已知等腰三角形ABC,顶点A的坐标是(
如图,已知等腰三角形ABC,顶点A的坐标是( 如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.