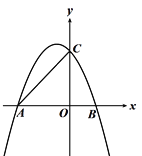题目内容
【题目】如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
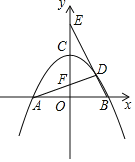
(1)当△ABD的面积为4时,
①求点D的坐标;
②联结OD,点M是抛物线上的点,且∠MDO=∠BOD,求点M的坐标;
(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)不变化,值为8,理由见解析
;(2)不变化,值为8,理由见解析
【解析】
(1)先将已知点B坐标代入解析式求出a,再根据△ABD的面积,求出D的纵坐标,将其代入抛物线求出D点坐标,根据∠MDO=∠BOD分两种情况讨论,并求出M坐标
(2)设出点D的坐标,利用平行线分线段成比例定理表示出OE、OF求和即可得出结论
(1)∵抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),
∴A(﹣2,0),4a+4=0,
∴a=﹣1,AB=4,
∴抛物线的解析式为y=﹣x2+4,
①设D(m,﹣m2+4),
∵△ABD的面积为4,
∴![]()
∴![]() ,
,
∵点D在第一象限,
∴![]() ,
,
∴![]() ,
,
②如图1,点M在OD上方时,
∵∠MDO=∠BOD,∴DM∥AB,
∴![]() ,当M在OD下方时,
,当M在OD下方时,
设DM交x轴于G,设G(n,0),
∴OG=n,
∵![]() ,
,
∴![]() ,
,
∵∠MDO=∠BOD,
∴OG=DG,
∴![]() ,
,
∴![]() ,
,
∴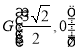 ,
,
∵![]() ,
,
∴直线DG的解析式为![]() ①,
①,
∵抛物线的解析式为y=﹣x2+4②,
联立①②得, ![]() ,此时交点刚好是D点,
,此时交点刚好是D点,
所以在OD下方不存在点M.
(2)OE+OF的值不发生变化,
理由:如图2,过点D作DH⊥AB于H,
∴OF∥DH,
∴![]() ,
,
设D(b,﹣b2+4),
∴AH=b+2,DH=﹣b2+4,
∵OA=2,
∴![]() ,
,
∴![]() ,
,
同理:OE=2(2+b),
∴OE+OF=2(2﹣b)+2(2+b)=8.

【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)