��Ŀ����
��2013•������һģ����֪����ƽ��ֱ������ϵxOy�У���A������Ϊ��0��2������P��m��n����������y=
x2+1�ϵ�һ�����㣮
��1����ͼ1��������P��PB��x�ᣬ����ΪB������PA����ͨ����������㣬�Ƚ�PA��PB�Ĵ�С��ϵ��PA
��2�������ã�1���Ľ��۽���������⣺
����ͼ2����C������Ϊ��2��5��������PC��AP+PC�Ƿ������Сֵ��������ڣ����P�����ꣻ��������ڣ���˵�����ɣ�
����ͼ3��������P��ԭ��O��ֱ�߽�����������һ��D����AP=2AD����ֱ��OP�Ľ���ʽ��
| 1 | 4 |
��1����ͼ1��������P��PB��x�ᣬ����ΪB������PA����ͨ����������㣬�Ƚ�PA��PB�Ĵ�С��ϵ��PA
=
=
PB��ֱ����д��������������=�������������̣�����2�������ã�1���Ľ��۽���������⣺
����ͼ2����C������Ϊ��2��5��������PC��AP+PC�Ƿ������Сֵ��������ڣ����P�����ꣻ��������ڣ���˵�����ɣ�
����ͼ3��������P��ԭ��O��ֱ�߽�����������һ��D����AP=2AD����ֱ��OP�Ľ���ʽ��

��������1�����������ľ��빫ʽ�����κ���ͼ���ϵ������������֪PA=PB��
��2������P��PB��x����B���ɣ�1����PA=PB������ҪʹAP+CP��С��ֻ�赱BP+CP��С����˵�C��P��B����ʱ��AP+PCȡ����Сֵ��
��3���������ۣ�����Pλ�ڵ�һ���͵ڶ����ޣ����Ե�Pλ�ڵ�һ�����з�������ͼ����DE��x����E����PF��x����F���������������Ρ�ODE�ס�OPF��������������εĶ�Ӧ�߳ɱ�������
=
=
��������P��m��
m2+1������D��
m��
m2+
�����ɣ�1���еĽ��۵õ���ʽ
m2+
=
(
m)2+1���ݴ˿�����õ�P������Ϊ��2
��3����������ֱ��OP�Ľ���ʽΪy=
x��
��2������P��PB��x����B���ɣ�1����PA=PB������ҪʹAP+CP��С��ֻ�赱BP+CP��С����˵�C��P��B����ʱ��AP+PCȡ����Сֵ��
��3���������ۣ�����Pλ�ڵ�һ���͵ڶ����ޣ����Ե�Pλ�ڵ�һ�����з�������ͼ����DE��x����E����PF��x����F���������������Ρ�ODE�ס�OPF��������������εĶ�Ӧ�߳ɱ�������
| OE |
| OF |
| DE |
| PF |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
3
| ||
| 4 |
���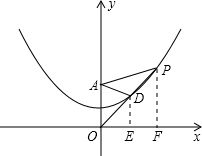 �⣺��1����ͼ���ߵ�A������Ϊ��0��2������P��m��n����
�⣺��1����ͼ���ߵ�A������Ϊ��0��2������P��m��n����
��AP2=m2+��n-2��2����
�ߵ�P��m��n����������y=
x2+1�ϵ�һ�����㣬
��n=
m2+1��
��m2=4n-4����
�ɢ٢�֪��AP=n��
�֡�PB��x�ᣬ
��PB=n��
��PA=PB��
���=��
��2���ٹ���P��PB��x����B���ɣ�1����PA=PB��
����ҪʹAP+CP��С��ֻ�赱BP+CP��С����˵�C��P��B����ʱȡ�ã�
��ʱ��P�ĺ�������ڵ�C��2��5���ĺ����꣬
���Ե�P������Ϊ��2��2����
�ڵ���P�ڵ�һ����ʱ����ͼ����DE��x����E����PF��x����F��
�ɣ�1���ã�DA=DE��PA=PF
��PA=2DA����PF=2DE��
�ߡ�ODE�ס�OPF����
=
=
��P��m��
m2+1������D��
m��
m2+
��
��
m2+
=
(
m)2+1�����m=��2
�ߵ�D��������y=
x2+1�ϣ�������ȥ��
��ʱP��2
��3����ֱ��OP�Ľ���ʽΪy=
x��
��P�ڵڶ�����ʱ��
ͬ�������ֱ��OP�Ľ���ʽΪy=-
x��
���ϣ�����ֱ��OP�Ľ���ʽΪy=
x��y=-
x��
 �⣺��1����ͼ���ߵ�A������Ϊ��0��2������P��m��n����
�⣺��1����ͼ���ߵ�A������Ϊ��0��2������P��m��n������AP2=m2+��n-2��2����
�ߵ�P��m��n����������y=
| 1 |
| 4 |
��n=
| 1 |
| 4 |
��m2=4n-4����
�ɢ٢�֪��AP=n��
�֡�PB��x�ᣬ
��PB=n��
��PA=PB��
���=��
��2���ٹ���P��PB��x����B���ɣ�1����PA=PB��
����ҪʹAP+CP��С��ֻ�赱BP+CP��С����˵�C��P��B����ʱȡ�ã�
��ʱ��P�ĺ�������ڵ�C��2��5���ĺ����꣬
���Ե�P������Ϊ��2��2����
�ڵ���P�ڵ�һ����ʱ����ͼ����DE��x����E����PF��x����F��
�ɣ�1���ã�DA=DE��PA=PF
��PA=2DA����PF=2DE��
�ߡ�ODE�ס�OPF����
| OE |
| OF |
| DE |
| PF |
| 1 |
| 2 |
��P��m��
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
��
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
�ߵ�D��������y=
| 1 |
| 4 |
��ʱP��2
| 2 |
3
| ||
| 4 |
��P�ڵڶ�����ʱ��
ͬ�������ֱ��OP�Ľ���ʽΪy=-
3
| ||
| 4 |
���ϣ�����ֱ��OP�Ľ���ʽΪy=
3
| ||
| 4 |
3
| ||
| 4 |
���������⿼���˶��κ����ۺ��⣮�����漰���˶��κ���ͼ���ϵ����������������ϵ������һ�κ�������ʽ�Լ���Գ�--·����������֪ʶ�㣮�����йض�������ʱҪע����������������۽����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2013•������һģ�����ǰѻ������ڰ뾶�����νеȱ����Σ���ͼ������OAB�ǵȱ����Σ���OA=R�����н����У��١�AOB=60�㣻�����ε��ܳ�Ϊ3R�������ε����Ϊ
��2013•������һģ�����ǰѻ������ڰ뾶�����νеȱ����Σ���ͼ������OAB�ǵȱ����Σ���OA=R�����н����У��١�AOB=60�㣻�����ε��ܳ�Ϊ3R�������ε����Ϊ