题目内容
 (2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为
(2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为| 1 |
| 2 |
分析:根据弧长的计算公式判断①错误;
根据扇形的周长定义判断②正确;
根据S扇形=
lR(其中l为扇形的弧长)判断③正确;
先由等边扇形的定义得出AB<OA,再根据等腰三角形三线合一的性质得出AM与OB不垂直,判断④错误;
由线段垂直平分线的性质及三角形两边之和大于第三边得出OP=PA>
OA,又OA=OC,OP+PC=OC,则PC<
OC<OP=AP,即PC<圆P的半径,判断⑤错误.
根据扇形的周长定义判断②正确;
根据S扇形=
| 1 |
| 2 |
先由等边扇形的定义得出AB<OA,再根据等腰三角形三线合一的性质得出AM与OB不垂直,判断④错误;
由线段垂直平分线的性质及三角形两边之和大于第三边得出OP=PA>
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①设∠AOB=n°,
∵OA=OB=
=R,
∴R=
,
∴n=
<60,故①错误;
②扇形的周长为:OA+OB+
=R+R+R=3R,故②正确;
 ③扇形的面积为:
③扇形的面积为:
•OA=
R•R=
R2,故③正确;
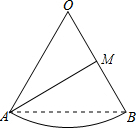
④如图,设半径OB的中点为M,连接AM.
∵OA=OB=
=R,
∴AB<R=OA,
∵OM=MB,
∴AM与OB不垂直,故④错误;
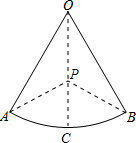 ⑤如图,设弧AB的中点为C.
⑤如图,设弧AB的中点为C.
∵OP=PA>
OA,
∵OA=OC,
∴OP>
OC,
∵OP+PC=OC,
∴PC<
OC<OP=AP,
即PC<圆P的半径,
∴以P为圆心,PA为半径作圆,则该圆一定不会经过扇形的弧AB的中点C.
故选B.
∵OA=OB=
 |
| AB |
∴R=
| nπR |
| 180 |
∴n=
| 180 |
| π |
②扇形的周长为:OA+OB+
 |
| AB |
 ③扇形的面积为:
③扇形的面积为:| 1 |
| 2 |
 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
④如图,设半径OB的中点为M,连接AM.
∵OA=OB=
 |
| AB |
∴AB<R=OA,
∵OM=MB,
∴AM与OB不垂直,故④错误;
 ⑤如图,设弧AB的中点为C.
⑤如图,设弧AB的中点为C.∵OP=PA>
| 1 |
| 2 |
∵OA=OC,
∴OP>
| 1 |
| 2 |
∵OP+PC=OC,
∴PC<
| 1 |
| 2 |
即PC<圆P的半径,
∴以P为圆心,PA为半径作圆,则该圆一定不会经过扇形的弧AB的中点C.
故选B.
点评:本题考查了弧长的计算,扇形的周长与面积,等腰三角形、线段垂直平分线的性质,三角形三边关系定理,三点共圆的条件,综合性较强,难度适中.

练习册系列答案
相关题目

