��Ŀ����
����Ŀ����ͼ1����O��������ABCD���Խ��ߵĽ���. �ֱ��ӳ�OD����G��OC����E��ʹOG=2OD��OE=2OC��Ȼ����OG��OEΪ�ڱ���������OEFG������AG��DE��
��1����֤��DE��AG��
��2��������ABCD�̶�����������OEFG�Ƶ�O��ʱ����ת![]() �ǣ�0��<
�ǣ�0��< ![]() <360�㣩�õ�������
<360�㣩�õ�������![]() ����ͼ2��
����ͼ2��
������ת�����У�����![]() ��ֱ��ʱ����
��ֱ��ʱ����![]() �Ķ�������ע������ֱ�DZ�Ϊб��һ��ʱ������ֱ�DZ����Ե����Ϊ30�ȣ�
�Ķ�������ע������ֱ�DZ�Ϊб��һ��ʱ������ֱ�DZ����Ե����Ϊ30�ȣ�
����������ABCD�ı߳�Ϊ1������ת�����У���![]() �������ֵ�ʹ�ʱ
�������ֵ�ʹ�ʱ![]() �Ķ�����ֱ��д���������˵�����ɣ�
�Ķ�����ֱ��д���������˵�����ɣ�
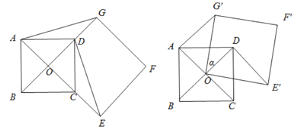
ͼ1 ͼ2
���𰸡���1��֤������������2���٣�1��30���150���AF�䳤�����ֵ��![]() ����ʱ��=315��.
����ʱ��=315��.
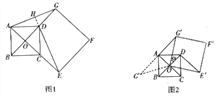
����������1����ͼ1���ӳ�ED��AG�ڵ�H��
��OΪ������ABCD�Խ��ߵĽ��㣮��OA=OD��OA��OD��
��OG=OE����Rt��AOG��Rt��DOE�����AGO=��DEO��
�ߡ�AGO+��GAO=90�㣬���DEO+��GAO=90�㣬���AHE=90�㣬��DE��AG��
��2��������ת�����У���![]() ��Ϊֱ�����������������
��Ϊֱ�����������������
��i������0������90������У�����![]() Ϊֱ��ʱ��
Ϊֱ��ʱ��
��![]() ������Rt��
������Rt��![]() ��
�� ![]() ��
��
���![]() ��OA��OD�����DOG��=90�㣭��
��OA��OD�����DOG��=90�㣭��![]() =30�㣬����=30�㣮
=30�㣬����=30�㣮
��ii������90������180������У�����![]() Ϊֱ��ʱ��
Ϊֱ��ʱ��
ͬ������ġ�AOG��=30�㣬������=90��+��![]() =150�㣮
=150�㣮
���ϣ�����![]() Ϊֱ��ʱ����=30���150�㣮
Ϊֱ��ʱ����=30���150�㣮
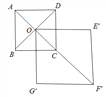
��AF�䳤�����ֵ��![]() ����ʱ��=315�㣮���ɣ���AF�䳤�����ʱ����F����ֱ��AC�ϣ���ͼ��ʾ��
����ʱ��=315�㣮���ɣ���AF�䳤�����ʱ����F����ֱ��AC�ϣ���ͼ��ʾ��
��AB=BC=CD=AD=1����AC=BD=![]() ��AO=OD=
��AO=OD=![]() ��
��
��OE��=E��F��=2OD=![]() ����OF��=
����OF��=![]() ����AF��=AO+OF��=
����AF��=AO+OF��=![]() ��
��
�ߡ�E��OF��=45�����ת����=360��-45��=315�㣮