Question

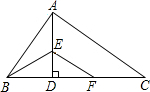如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论一定成立的是

1. A.
   AB=BF
2. B.
   AE=ED
3. C.
   AD=DC
4. D.
   ∠ABE=∠DFE

Answer 1

A
分析：从已知条件思考，利用角平分线的性质，结合平行线的性质，可得很多结论，然后与选项进行逐个比对，答案可得．
解答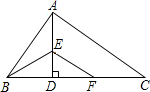：解：∵∠BAD+∠ABD=90°，∠ABD+∠C=90°
∴∠BAD=∠C（同角的余角相等）
又∵EF∥AC
∴∠BFE=∠C
∴∠BAD=∠BFE
又∵BE平分∠ABC
∴∠ABE=∠FBE
∴∠BEF=∠AEB，
在△ABE与△FBE中，
∵
∴△ABE≌△FBE（AAS）
∴AB=BF．
故选A．
点评：此题考查角平分线的定义，平行线的性质，同角的余角相等，三角形全等的判定等知识点．