题目内容
(10分)已知方程组 的解x为非正数,y 为负数.
的解x为非正数,y 为负数.
(1)求a的取值范围;
(2)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
19.
【答案】
①  ②
② 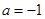
【解析】
试题分析:(1)题: ,由(1)+(2)得1+3a-7-a=2x,∴a=x+3.
,由(1)+(2)得1+3a-7-a=2x,∴a=x+3.
已知x为非正数,即x≤0,所以x+3≤3,a≤3。
由(2)-(1)得:-7-a-1-3a=2y,∴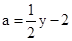 ,
,
已知y 为负数,即y<0.所以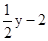 <-2.所以a<-2.综合可得
<-2.所以a<-2.综合可得
(2)题:2ax+x>2a+1化简得(x-1)(2a-1)>0.已知解为x<1,∴x-1<0.∴2a-1<0,解得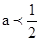 。
。
由(1)题知 ,且
,且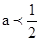 。所以a为整数可取:a=-1。
。所以a为整数可取:a=-1。
考点:不等式
点评:本题难度较高。主要考查学生综合二元一次方程组解不等式。关键:消元法。

练习册系列答案
相关题目
 的解x为非正数,y 为负数.
的解x为非正数,y 为负数. 的解x为非正数,y 为负数.
的解x为非正数,y 为负数.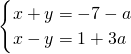 的解x为非正数,y为负数.
的解x为非正数,y为负数.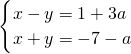 的解x为非正数,y为负数.求a的取值范围.
的解x为非正数,y为负数.求a的取值范围.