题目内容
已知方程组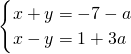 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1?
解:(1)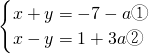
∵①+②得:2x=-6+2a,
x=-3+a,
①-②得:2y=-8-4a,
y=-4-2a,
∵方程组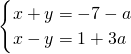 的解x为非正数,y为负数,
的解x为非正数,y为负数,
∴-3+a≤0且-4-2a<0,
解得:-2<a≤3;
(2)∵-2<a≤3,
∴|a-3|+|a+2|
=3-a+a+2
=5;
(3)2ax+x>2a+1,
(2a+1)x>2a+1,
∵不等式的解为x<1
∴2a+1<0,
∴a<- ,
,
∵-2<a≤3,
∴a的值是-1,
∴当a为-1时,不等式2ax+x>2a+1的解为x<1.
分析:(1)求出不等式组的解集即可得出关于a的不等式组,求出不等式组的解集即可;
(2)根据a的范围去掉绝对值符号,即可得出答案;
(3)求出a<- ,根据a的范围即可得出答案.
,根据a的范围即可得出答案.
点评:本题考查了解方程组和解不等式组的应用,主要考查学生的理解能力和计算能力,题目比较好.
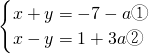
∵①+②得:2x=-6+2a,
x=-3+a,
①-②得:2y=-8-4a,
y=-4-2a,
∵方程组
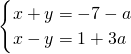 的解x为非正数,y为负数,
的解x为非正数,y为负数,∴-3+a≤0且-4-2a<0,
解得:-2<a≤3;
(2)∵-2<a≤3,
∴|a-3|+|a+2|
=3-a+a+2
=5;
(3)2ax+x>2a+1,
(2a+1)x>2a+1,
∵不等式的解为x<1
∴2a+1<0,
∴a<-
 ,
,∵-2<a≤3,
∴a的值是-1,
∴当a为-1时,不等式2ax+x>2a+1的解为x<1.
分析:(1)求出不等式组的解集即可得出关于a的不等式组,求出不等式组的解集即可;
(2)根据a的范围去掉绝对值符号,即可得出答案;
(3)求出a<-
 ,根据a的范围即可得出答案.
,根据a的范围即可得出答案.点评:本题考查了解方程组和解不等式组的应用,主要考查学生的理解能力和计算能力,题目比较好.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的解x为非正数,y 为负数.
的解x为非正数,y 为负数. 的解x为非正数,y 为负数.
的解x为非正数,y 为负数. 的解x为非正数,y 为负数.
的解x为非正数,y 为负数.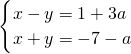 的解x为非正数,y为负数.求a的取值范围.
的解x为非正数,y为负数.求a的取值范围.