Question

【题目】已知，如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC=BC，AC= OB．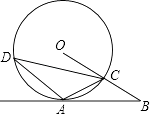
（1）求证：AB是⊙O的切线；
（2）若∠ACD=45°，OC=2，求弦AD的长．

Answer 1

【答案】
（1）证明：如图连接OA．

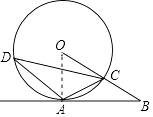
∵AC= OB，OC=CB，

∴AC=OC=CB，

∴∠OAB=90°，

∴AB是⊙O的切线．

（2）解：连接OD．

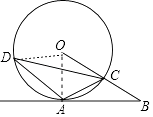
∵∠DAO=2∠DCA，∠DCA=45°，

∴∠DOA=90°，∵OD=OA=OC=2，

∴AD= = =2 ．

【解析】（1）根据如果一个三角形一边上的中线等于这边的一半，这个三角形是直角三角形，即可判断∠OAB=90°，即可解决问题．（2）只要证明∠DOA=90°，利用勾股定理即可解决问题．