题目内容
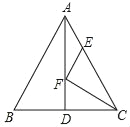
【题目】如图,△ABC中,AB=AC=5,BC=6,AD⊥BC,E、F分别为AC、AD上两动点,连接CF、EF,则CF+EF的最小值为____.
【答案】![]()
【解析】
作BM⊥AC于M,交AD于F,根据三线合一定理求出BD的长和AD⊥BC,根据三角形面积公式求出BM,根据对称性质求出BF=CF,根据垂线段最短得出CF+EF≥BM,即可得出答案.
作BM⊥AC于M,交AD于F,
∵AB=AC=5,BC=6,AD是BC边上的中线,
∴BD=DC=3,AD⊥BC,AD平分∠BAC,
∴B、C关于AD对称,
∴BF=CF,
根据垂线段最短得出:CF+EF=BF+EF≥BF+FM=BM,
即CF+EF≥BM,
∵S△ABC=![]() ×BC×AD=
×BC×AD=![]() ×AC×BM,
×AC×BM,
∴BM=![]() ,
,
即CF+EF的最小值是![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
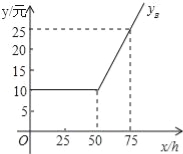
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?