题目内容
【题目】如图，已知在平面直角坐标系中，O是坐标原点，点A（2，5）在反比例函数y= 
的图象上．一次函数y=x+b的图象过点A，且与反比例函数图象的另一交点为B．
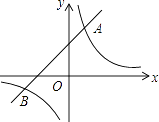
（1）求k和b的值；
（2）设反比例函数值为y1 ， 一次函数值为y2 ， 求y1＞y2时x的取值范围．
【答案】
（1）
解：把A（2，5）分别代入y= 
和y=x+b，
得 
，
解得k=10，b=3；
（2）
解：由（1）得，直线AB的解析式为y=x+3，
反比例函数的解析式为y= 
．
由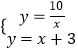 
，解得： 
或 
．
则点B的坐标为（﹣5，﹣2）．
由图象可知，当y1＞y2时，x的取值范围是x＜﹣5或0＜x＜2．
【解析】本题主要考查了反比例函数与一次函数的交点问题，解题的关键是求出k和b的值，此题难度不大．（1）把A（2，5）分别代入y= 和y=x+b，即可求出k和b的值；（2）联立一次函数和反比例函数的解析式，求出交点坐标，进而结合图形求出y1＞y2时x的取值范围．
练习册系列答案
阅读快车系列答案
相关题目
