题目内容
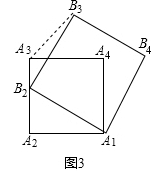
【题目】如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于 . 
【答案】![]() 或
或 ![]() 或
或 ![]()
【解析】解:∵矩形ABCD中,AB=1,AD=2,E是AD中点, ∴∠BAD=90°,AE=DE=1,
∴△ABE是等腰直角三角形,
∴BE= ![]() AB=
AB= ![]() .
.
若△BEP为等腰三角形,则分三种情况:①当BP=BE时,显然BP= ![]() ;②当PB=PE时,如图,连结AP.
;②当PB=PE时,如图,连结AP.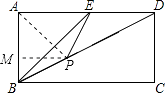
∵PB=PE,AB=AE,
∴AP垂直平分BE,
∵△ABE是等腰直角三角形,
∴∠BAP=∠EAP=45°.
作PM⊥AB于M,设PM=x,
∵S△ABD=S△ABP+S△APD
∴ ![]() ×1x+
×1x+ ![]() ×2x=
×2x= ![]() ×1×2,
×1×2,
解得x= ![]() ,
,
∴PM= ![]() ,
,
∴BP= ![]() =
= ![]() =
= ![]() ;③当EB=EP时,如图,过A作AF⊥BD于F,
;③当EB=EP时,如图,过A作AF⊥BD于F,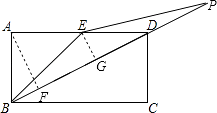
过E作EG⊥BD于G.
在Rt△ABF中,AF=ABsin∠ABF=1× ![]() =
= ![]() ,
,
∵AE=ED,EG∥AF,
∴EG= ![]() AF=
AF= ![]() .
.
在Rt△BEG中,∵BE= ![]() ,EG=
,EG= ![]() ,
,
∴BG= ![]() =
= ![]() .
.
∵EB=EP,EG⊥BP,
∴BP=2BG= ![]() .
.
综上所述,线段BP的长度等于 ![]() 或
或 ![]() 或
或 ![]() .
.
故答案为 ![]() 或
或 ![]() 或
或 ![]() .
.
先根据矩形的性质及中点的定义得出∠BAD=90°,AE=DE=1,那么△ABE是等腰直角三角形,BE= ![]() AB=
AB= ![]() .再分三种情况讨论:①BP=BE;②PB=PE;③EB=EP.
.再分三种情况讨论:①BP=BE;②PB=PE;③EB=EP.

【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果). 
【题目】某公司要把240吨白砂糖运往某市的A、B两地,用大小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种大小货车的载重分别是15吨/辆和10吨/辆,运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.
(1)求大小两种货车各多少辆.
(2)如果安排10辆货车前往A地,其中调往A地的大货车有a辆,其余货车前往B地,填写下表:
前往A地 | 前往B地 | |
大货车/辆 | a | |
小货车/辆 |
(3)按照上表的分配方案,若设总费用为W,求W与a的关系式(用含a的代数式表示W)