��Ŀ����
����Ŀ���Ķ�����
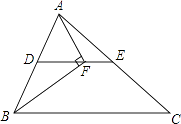
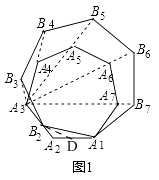
��ͼ��1�������������A1A2A3��An�ı�A2A3����ȡһ�����A2�غϵĵ�B2 �� �����߶�A1B2Ϊ�����߶�A1A2���Ϸ������������A1B2B3��Bn �� ���������A1B2B3��Bn���������A1A2��An��λ��ͼ�Σ���A3��Ϊλ�����ģ�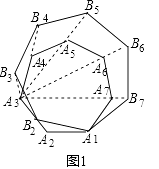
������֤
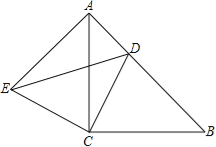
��1����ͼ��2����֪��������A1A2A3��λ��ͼ��Ϊ��������A1B2B3 �� ��֤�������ŵ�B2���˶�����B3A3A1�Ĵ�Сʼ�ղ��䣮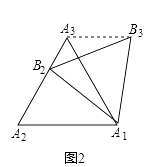
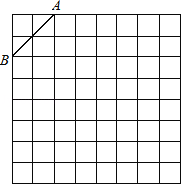
��2����ͼ��3����֪������A1A2A3A4��λ��ͼ��Ϊ������A1B2B3B4 �� ���ŵ�B2���˶�����B3A3A4�Ĵ�Сʼ�ղ��䣿�����䣬�������B3A3A4�Ĵ�С�����ı䣬��˵�����ɣ�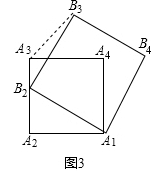
��3����ͼ��1��������£�
���Բ����B3A3A4�Ĵ�С�Ƿ�ᷢ���ı䣿�����ı䣬���ú�n�Ĵ���ʽ��ʾ����B3A3A4�Ĵ�С��ֱ��д������������ı䣬��˵�����ɣ�
�١�B3A3A4+��B4A4A5+��B5A5A6+��+��BnAnA1= ![]() ���ú�n�Ĵ���ʽ��ʾ��
���ú�n�Ĵ���ʽ��ʾ��
���𰸡�
��1��
֤�����ߡ�A1A2A3���A1B2B3���������Σ�
��A1A2=A1A3��A1B2=A1B3����A2A1A3=��B2A1B3=60�㣬
���A2A1B2=��A3A1B3��
���A2A1B2�ա�A3A1B3��
���B3A3A1=��A2=60�㣬
���B3A3A1�Ĵ�С����
��ѧ˼��
��2��
�⣺��B3A3A4�Ĵ�С���䣬
���ɣ���ͼ���ڱ�A1A2��ȡһ��D��ʹA1D=A3B2������B2D��
���ı���A1A2A3A4��A1B2B3B4�������Σ�
��A1B2=B2B3����A1B2B3=��A1A2A3=90�㣬
���A3B2B3+��A1B2A2=90�㣬��A2A1B2+��A1B2A2=90�㣬
���A3B2B3=��A2A1B2��
���A3B2B3�ա�DA1B2��
���B2A3B3=��A1DB2��
��A1A2=A2A3��A1D=A3B2��
��A2B2=A2D��
�ߡ�A1A2A3=90�㣬
���DA2B2�ǵ���ֱ�������Σ�
���A1DB2=135�㣬
���B2A3B3=135�㣬
�ߡ�A4A3A2=90�㣬
���B3A3A4=45�㣬
������B3A3A4�Ĵ�Сʼ�ղ���
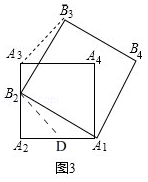
���ɲ���
��3��
�⣺�١�B3A3B4�Ĵ�Сʼ�ղ��䣬���ɣ���ͼ1��
��A1A2��ȡһ��D��ʹA1D=A3B2��
����B2D��
�ߡ�A2A1B2=180�㩁��A1B2A2����A3B2B3=180�㩁��A1B2A2��
���A2A1B2=��A3B2B3��
��A1B2=B2B3��
���A3B2B3�ա�DA1B2��
���B2A3B3=A1DB2��
��A1A2=A2A3��A1D=A3B2��
��A2D=A2B2��
���A1DB2= ![]() ��180�㩁��A1A2B2��=90�㩁
��180�㩁��A1A2B2��=90�㩁 ![]() ��
�� ![]() =90�㩁
=90�㩁 ![]()
���B3A3A4=��A1DB2����B2A3A4=90�㩁 ![]() ��
�� ![]() =
= ![]()
���ɢ�֪����B3A3A4= ![]() ��
��
ͬ�ٵķ����ɵã���B4A4A5= ![]() ��2����B5A5A6=
��2����B5A5A6= ![]() ��3��������BnAnA1=
��3��������BnAnA1= ![]() ����n��2����
����n��2����
��١�B3A3A4+��B4A4A5+��B5A5A6+��+��BnAnA1
= ![]() +
+ ![]() ��2+
��2+ ![]() ��3+��
��3+�� ![]() ����n��2��=
����n��2��= ![]() ��
��
�ʴ�Ϊ ![]() ��
��
����������1�����жϳ���A2A1B2�ա�A3A1B3 �� �����õȱ������ε����ʼ��ɵó����ۣ���2�����жϳ���A3B2B3�ա�DA1B2 �� �����������ε����ʼ��ɵó����ۣ���3�������жϳ���A3B2B3�ա�DA1B2 �� ������������εı���Ⱥ�ÿ���ڽǼ��ɵó����ۣ������âٵĽ��ۺͷ������ɵó����ۣ�
�����㾫����������Ĺؼ���������ȱ������ε����ʵ����֪ʶ�����յȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�㣮

 ������ϵ�д�
������ϵ�д�