题目内容
在△ABC中，AB=AC=4，BC=2，则4cosB等于
- A.1
- B.2
- C.
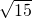
- D.
A
分析：在等腰三角形中，过顶点A作出底边BC上的高AD．就可以运用三线合一定理，在直角△ABD中，根据三角函数的定义就可以求解．
解答：
解：过顶点A作出底边BC上的高AD，垂足为D．
根据等腰三角形的性质知，BD=1．
∴4cosB=4×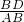
=4×
=1．
故选A．
点评：本题考查了锐角三角函数的定义和利用了等腰三角形的性质．
分析：在等腰三角形中，过顶点A作出底边BC上的高AD．就可以运用三线合一定理，在直角△ABD中，根据三角函数的定义就可以求解．
解答：
解：过顶点A作出底边BC上的高AD，垂足为D．根据等腰三角形的性质知，BD=1．
∴4cosB=4×
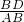=4×=1．故选A．
点评：本题考查了锐角三角函数的定义和利用了等腰三角形的性质．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
（2013•宁德质检）如图，在△ABC中，AB=AC=6，点0为AC的中点，OE⊥AB于点E，OE=
（2012•襄阳）如图，在△ABC中，AB=AC，AD⊥BC于点D，将△ADC绕点A顺时针旋转，使AC与AB重合，点D落在点E处，AE的延长线交CB的延长线于点M，EB的延长线交AD的延长线于点N．
如图，在△ABC中，AB=AC，把△ABC绕着点A旋转至△AB1C1的位置，AB1交BC于点D，B1C1交AC于点E．求证：AD=AE．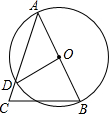
（2013•滨湖区一模）如图，在△ABC中，AB是⊙O的直径，∠B=60°，∠C=70°，则∠BOD的度数是（ ）
（2012•吉林）如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作?ABDE，连接AD，EC．