Question

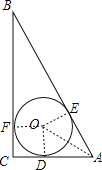
【题目】如图，⊙O为Rt△ABC的内切圆，⊙O的半径r=1，∠B=30°，

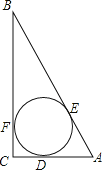
（1）劣弧DE的长．

（2）证明：AD=AE．

（3）求：劣弧DE、切线AD、AE所围成的面积S．

Answer 1

【答案】（1）（2）证明见解析（3）﹣

【解析】

试题分析：（1）根据切线的性质得出OD⊥AC，OE⊥AB，根据四边形内角和求得∠DOE=120°，代入公式求得即可；

（2）证得RT△AOD≌RT△AOE即可得到结论；

（3）根据S=S四边形ADOE﹣S扇形ODE求得即可．

解：（1）连接OD、OE，则OD⊥A，COE⊥AB

∵∠B=30°∠C=90°

∴∠A=60°

∴∠DOE=120°

劣弧DE的长=；

（2）连接OA，

在RT△AOD和RT△AOE中

∴RT△AOD≌RT△AOE（HL），

∴AD=AE

（3）∵RT△AOD≌RT△AOE，

∴∠OAB=∠OAC=∠BAC=30°，

∴AE=OE=，

∴四边形ADOE的面积=2×AEOE=，

∵S扇形ODE==π

∴S=S四边形ADOE﹣S扇形ODE=﹣．