题目内容
【题目】如图，防洪大堤的横截面ABGH是梯形，背水坡AB的坡度i=1：
（垂直高度AE与水平宽度BE的比），AB=20米，BC=30米，身高为1.7米的小明（AM=1.7米）站在大堤A点（M，A，E三点在同一条直线上），测得电线杆顶端D的仰角∠
=20°．
（1）求∠ABC；
（2）求电线杆CD的高度．（结果精确到个位，参考数据sin20°≈0.3，cos20°≈0.9，tan20°≈0.4，≈1.7）
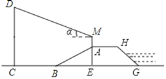
【答案】(1)150°;(2)31米.
【解析】
（1）根据坡度的定义，利用三角函数即可求得坡角，再求出∠ABC即可；
（2）由i的值求得大堤的高度h，点A到点B的水平距离a，从而求得MN的长度，由仰角求得DN的高度，从而由DN，AM，h求得高度CD．
解：（1）∵i=1：
∴tan∠ABE=i=1：
∴∠ABE=30°
∴∠ABC=150°
（2）过M点作MN垂直于CD的于点N．
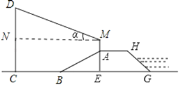
∵AB=20m，∠ABE=30°,
∴AE=
AB=×20=10，
BE=ABcos30°=20×
=10，
∴CN=AE+AM=10+1.7=11.7，
MN=CB+BE=30+10，
∵∠NMD=20°，MN=30+10，
∴DN=MNtan20°=（30+10）×0.4=12+4，
∴CD=CN+DN=11.7+12+4=23.7+4≈31．
答：电线杆CD的高度约为31米．
练习册系列答案
相关题目
