题目内容
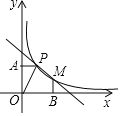
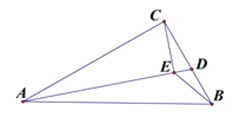
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是( )
A.2.5B.![]()
![]() C.
C.![]() D.5
D.5
【答案】C
【解析】
由∠AEC=90°知E在以AC为直径的⊙M的![]() 上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
解:如图,取AC的中点M,以AC为直径作圆M,交AB于点N,连接BM,交圆M于点E′,过M作MF⊥AB于点F,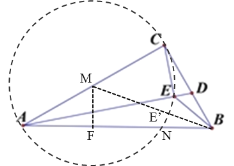
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的![]() 上(不含点C、可含点N),
上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=13cm,AC=12cm,BC=5cm,
∴AC2+BC2=AB2,AM=CM=6
∴∠ACB=90°,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴![]() ,即
,即![]() ,解得:MF=
,解得:MF=![]() ,
,
∴AF=![]() ,
,
则BF=ABAF=![]() ,
,
∴BM=![]() ,
,
∵ME=6,
∴BE长度的最小值BE′=BMME′=![]() ,
,
故答案为:C.

练习册系列答案
相关题目