题目内容
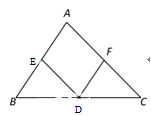
【题目】如图,在Rt△ABC中,∠ACB=90°,AC的垂直平分线EF交AC于点D,交AB于点F,且CE=BF.
(1)求证:四边形AECF是菱形;
(2)当∠BAC的度数为多少时,四边形AECF是正方形.

【答案】(1)证明见详解;(2)∠BAC=45![]() .
.
【解析】
(1) 根据中垂线的性质:中垂线上的点到线段两个端点的距离相等, 有BE=EC, BF=FC, 根据四边相等的四边形是菱形即可判断;
(2)由菱形的性质知,对角线平分一组对角,即当∠BAC=45![]() 时,∠EAF=90
时,∠EAF=90![]() ,则菱形AECF为正方形.
,则菱形AECF为正方形.
证明: (1) 
![]() AC的垂直平分线EF交AC于点D
AC的垂直平分线EF交AC于点D
![]() CD=AD,∠ADF=90
CD=AD,∠ADF=90![]() ,EC=AE,CF=AF,
,EC=AE,CF=AF,
![]() 又∠ACB=90°,
又∠ACB=90°,![]() EF∥BC,
EF∥BC,
![]() △ADF∽△ACB,
△ADF∽△ACB,
![]() AF:AB=AD:AC,
AF:AB=AD:AC, ![]() CD=AD,D为AC的中点,
CD=AD,D为AC的中点,
![]() AF:AB=AD:AC=1:2,
AF:AB=AD:AC=1:2,
![]() F为AB中点,
F为AB中点,
![]() BF=AF,在Rt△ABC中,∠ACB=90°,
BF=AF,在Rt△ABC中,∠ACB=90°, ![]() CF=AF,
CF=AF,
又![]() CE=BF, CF=AF, EC=AE,CF=AF
CE=BF, CF=AF, EC=AE,CF=AF
![]() CE= CF= AF= AE
CE= CF= AF= AE
![]() 四边形BECF是菱形.
四边形BECF是菱形.
(2)当∠BAC=45![]() 时, 四边形AECF是正方形.
时, 四边形AECF是正方形.
证明:![]() ∠BAC=45
∠BAC=45![]() ,四边形AECF是菱形,
,四边形AECF是菱形,
![]() ∠EAC=∠BAC=45
∠EAC=∠BAC=45![]() ,
,
![]() ∠EAF =∠EAC+∠BAC =90
∠EAF =∠EAC+∠BAC =90![]() ,
,
![]() 菱形AECF是正方形.
菱形AECF是正方形.

练习册系列答案
相关题目