题目内容
如图,△ABC是等腰直角三角形,AB=2,以AB为直径作⊙O,P为线段AB延长线上一动点.连接PC,将△CBP绕点C逆时针旋转90°的到△CAD.
(1)如图1所示,证明:AD为⊙O的切线.
(2)当BP=OB时,如图2所示,证明:AB平分线段CD.
(3)当BP=t•OB时(t?1)时,讨论以BP为半径的⊙B和⊙O位置关系,并求出相应t的取值范围.
(4)当BP=2OB时,请连接PD,试判断直线PD与⊙O的位置关系,并说明理由.
(1)如图1所示,证明:AD为⊙O的切线.
(2)当BP=OB时,如图2所示,证明:AB平分线段CD.
(3)当BP=t•OB时(t?1)时,讨论以BP为半径的⊙B和⊙O位置关系,并求出相应t的取值范围.
(4)当BP=2OB时,请连接PD,试判断直线PD与⊙O的位置关系,并说明理由.

分析:(1)根据等腰直角三角形的性质得CB=CA,∠CBA=∠CAB=45°,则由三角形外角性质得∠P+∠PCB=45°,再根据旋转的性质得∠PCB=∠DCA,∠P=∠D,则∠D+∠DCA=45°,于是根据三角形内角和定理可得到∠OAD=90°,然后根据切线的判定定理即可AD为⊙O的切线;
(2)连结OC,CD与AB交于Q,由AB为⊙O的直径和等腰直角三角形的性质得OC⊥AB,OC=OB,再根据旋转的性质得PB=AD,而BP=OB,于是OC=AD,则可根据“AAS”可判断△COQ≌△DAQ,所以CQ=DQ;
(3)根据圆与圆的位置关系得到当⊙B与⊙O相交时,OB<BP<2OB;当⊙B与⊙O内切时,BP=2OB;当⊙B与⊙O内含时,OB<BP<2OB,然后把PB=t•OB代入可分别得到t的取值范围或值;
(4)作OH⊥PD于H,设⊙O的半径为R,易得BP=2OB=2R,AD=2R,PA=4R,利用勾股定理可计算出PD=2
R,再证明Rt△POH∽Rt△PDA,利用相似比可得到OH=
R,所以OH>R,然后根据直线与圆的位置关系的判定方法得到直线PD与⊙O相离.
(2)连结OC,CD与AB交于Q,由AB为⊙O的直径和等腰直角三角形的性质得OC⊥AB,OC=OB,再根据旋转的性质得PB=AD,而BP=OB,于是OC=AD,则可根据“AAS”可判断△COQ≌△DAQ,所以CQ=DQ;
(3)根据圆与圆的位置关系得到当⊙B与⊙O相交时,OB<BP<2OB;当⊙B与⊙O内切时,BP=2OB;当⊙B与⊙O内含时,OB<BP<2OB,然后把PB=t•OB代入可分别得到t的取值范围或值;
(4)作OH⊥PD于H,设⊙O的半径为R,易得BP=2OB=2R,AD=2R,PA=4R,利用勾股定理可计算出PD=2
| 5 |
3
| ||
| 5 |
解答:(1)证明:∵△ABC是等腰直角三角形,
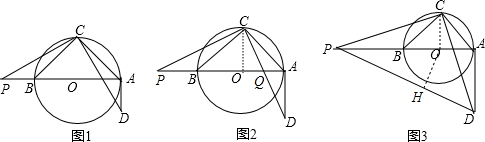 ∴CB=CA,∠CBA=∠CAB=45°,
∴CB=CA,∠CBA=∠CAB=45°,
∴∠P+∠PCB=∠CBA=45°,
∵△CBP绕点C逆时针旋转90°得到△CAD,
∴∠PCB=∠DCA,∠P=∠D,
∴∠D+∠DCA=45°,
∴∠D+∠DCA+∠CAB=90°,
∴∠OAD=90°,
∴OA⊥AD,
∴AD为⊙O的切线;
(2)证明:连结OC,CD与AB交于Q,如图2,
∵△ABC是等腰直角三角形,AB为⊙O的直径,
∴OC⊥AB,OC=OB,
而AD⊥AD,
∴∠COQ=∠DAQ=90°,
∵△CBP绕点C逆时针旋转90°得到△CAD,
∴PB=AD,
而BP=OB,
∴OC=AD,
在△COQ和△DAQ中,
,
∴△COQ≌△DAQ(AAS),
∴CQ=DQ,
即AB平分线段CD;
(3)当⊙B与⊙O相交时,OB<BP<2OB,即OB<t•OB<2OB,所以1<t<2;
当⊙B与⊙O内切时,BP=2OB,即t•OB=2OB,即t=2;
当⊙B与⊙O内含时,OB<BP<2OB,即OB<t•OB<2OB,所以t>2;
(4)直线PD与⊙O相离.理由如下:
作OH⊥PD于H,设⊙O的半径为R,如图3,
∵BP=2OB=2R,
∴AD=PB=2R,PA=4R,
∴PD=
=2
R,
∵∠OPH=∠DPA,
∴Rt△POH∽Rt△PDA,
∴OH:AD=PO:PD,即OH:2R=3R:2
R,
∴OH=
R>R,
∴直线PD与⊙O相离.
 ∴CB=CA,∠CBA=∠CAB=45°,
∴CB=CA,∠CBA=∠CAB=45°,∴∠P+∠PCB=∠CBA=45°,
∵△CBP绕点C逆时针旋转90°得到△CAD,
∴∠PCB=∠DCA,∠P=∠D,
∴∠D+∠DCA=45°,
∴∠D+∠DCA+∠CAB=90°,
∴∠OAD=90°,
∴OA⊥AD,
∴AD为⊙O的切线;
(2)证明:连结OC,CD与AB交于Q,如图2,
∵△ABC是等腰直角三角形,AB为⊙O的直径,
∴OC⊥AB,OC=OB,
而AD⊥AD,
∴∠COQ=∠DAQ=90°,
∵△CBP绕点C逆时针旋转90°得到△CAD,
∴PB=AD,
而BP=OB,
∴OC=AD,
在△COQ和△DAQ中,
|
∴△COQ≌△DAQ(AAS),
∴CQ=DQ,
即AB平分线段CD;
(3)当⊙B与⊙O相交时,OB<BP<2OB,即OB<t•OB<2OB,所以1<t<2;
当⊙B与⊙O内切时,BP=2OB,即t•OB=2OB,即t=2;
当⊙B与⊙O内含时,OB<BP<2OB,即OB<t•OB<2OB,所以t>2;
(4)直线PD与⊙O相离.理由如下:
作OH⊥PD于H,设⊙O的半径为R,如图3,
∵BP=2OB=2R,
∴AD=PB=2R,PA=4R,
∴PD=
| PA2+AD2 |
| 5 |
∵∠OPH=∠DPA,
∴Rt△POH∽Rt△PDA,
∴OH:AD=PO:PD,即OH:2R=3R:2
| 5 |
∴OH=
3
| ||
| 5 |
∴直线PD与⊙O相离.
点评:本题考查了圆的综合题:熟练掌握直线与圆的位置关系、圆与圆的位置关系以及判定方法;学会运用勾股定理和相似比进行几何计算;同时理解等腰直角三角形的性质和旋转的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( ) 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.