题目内容
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当 ![]() 时,求m的值.
时,求m的值.
【答案】
(1)解:由题意有△=(2m﹣1)2﹣4m2≥0,解得, ![]() .
.
即实数m的取值范围是 ![]() .
.
(2)解:由 ![]() 得(x1+x2)(x1﹣x2)=0,
得(x1+x2)(x1﹣x2)=0,
若x1+x2=0,即﹣(2m﹣1)=0,解得 ![]() .
.
∵ ![]() >
> ![]() ,
,
∴ ![]() 不合题意,舍去
不合题意,舍去
若x1﹣x2=0,即x1=x2,
∴△=0,由(1)知 ![]() .
.
故当 ![]() 时,
时, ![]() .
.
【解析】(1)根据题意可知原方程由两个实数根,则b2-4ac≥0,建立不等式求解即可。
(2) 先将x 1 2 x 2 2 = 0,转化为(x1+x2)(x1﹣x2)=0,再分情况:若x1+x2=0;若x1﹣x2=0,建立方程求解,再根据m的取值范围求出符合条件的m的值。
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
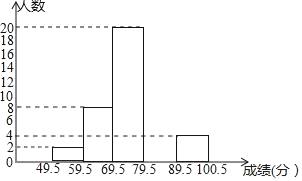
名牌中学课时作业系列答案【题目】某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末考试数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是 ;
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | 8 | 20 | a | 4 | c |
频率 | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |