题目内容
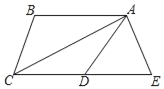
【题目】如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 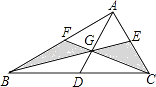
【答案】4
【解析】方法1
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE= ![]() S△ACF,S△BGF=S△BGD=
S△ACF,S△BGF=S△BGD= ![]() S△BCF,
S△BCF,
∵S△ACF=S△BCF= ![]() S△ABC=
S△ABC= ![]() ×12=6,
×12=6,
∴S△CGE= ![]() S△ACF=
S△ACF= ![]() ×6=2,S△BGF=
×6=2,S△BGF= ![]() S△BCF=
S△BCF= ![]() ×6=2,
×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.方法2
设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为S1,S2,S3,S4,S5,S6,根据中线平分三角形面积可得:S1=S2,S3=S4,S5=S6,S1+S2+S3=S4+S5+S6①,S2+S3+S4=S1+S5+S6②
由①﹣②可得S1=S4,所以S1=S2=S3=S4=S5=S6=2,故阴影部分的面积为4.
根据三角形的中线把三角形的面积分成相等的两部分,知△ABC的面积即为阴影部分的面积的3倍.

练习册系列答案
相关题目