题目内容
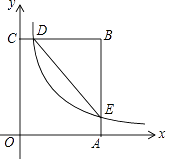
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y= ![]() (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 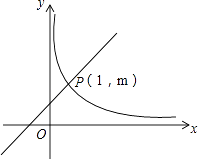
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
【答案】
(1)解:把P(1,m)代入y= ![]() ,得m=2,
,得m=2,
∴P(1,2)
把(1,2)代入y=kx+1,得k=1
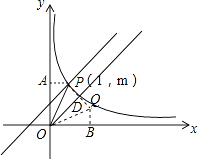
(2)解:如图所示:过点P作PA⊥y轴于点A,过点Q作QB⊥x轴于点B,
∵点Q与点P关于y=x成轴对称,OP=OQ,
∴∠POD=∠DOQ,∠AOD=∠BOD=45°,
∴∠AOP=∠BOQ,
在△APO和△BQO中,
 ,
,
∴△APO≌△BQO(AAS),
∴AO=OB=2,AP=QB=1,
∴Q点的坐标为:(2,1).
(3)解:设抛物线的解析式为y=ax2+bx+c,得:
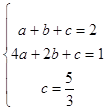 ,
,
解得  ,
,
故抛物线解析式为:y=﹣ ![]() x2+x+
x2+x+ ![]() ,
,
则对称轴方程为x=﹣ ![]() =
= ![]() .
.
【解析】(1)直接将P点代入反比例函数解析式得出m的值,进而把P点代入一次函数解析式得出答案;(2)利用全等三角形的判定和性质得出△APO≌△BQO(AAS),即可得出Q点坐标;(3)直接利用待定系数法求出二次函数解析式进而得出答案.

练习册系列答案
相关题目