题目内容
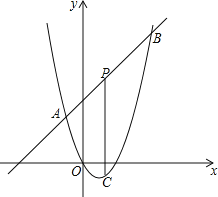
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点,抛物线的顶点为
两点,抛物线的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求此抛物线的解析式;
(2)求![]() 的面积;
的面积;
(3)在抛物线上是否存在一点![]() ,使它到
,使它到![]() 轴的距离为4,若存在,请求出点
轴的距离为4,若存在,请求出点![]() 的坐标,若不存在,则说明理由.
的坐标,若不存在,则说明理由.
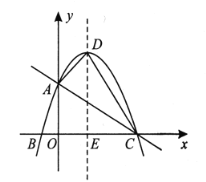
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)
x+2;(2)![]() ;(3)存在一点P
;(3)存在一点P![]() 或
或![]() ,使它到x轴的距离为4
,使它到x轴的距离为4
【解析】
(1)先根据一次函数的解析式求出A和C的坐标,再将点A和点C的坐标代入二次函数解析式即可得出答案;
(2)先求出顶点D的坐标,再过D点作DM平行于y轴交AC于M,再分别以DM为底求△ADM和△DCM的面积,相加即可得出答案;
(3)令y=4或y=-4,求出x的值即可得出答案.
解:(1)直线y=﹣![]() x+2中,当x = 0时,y = 2;
x+2中,当x = 0时,y = 2;
当y=0时,0 =﹣![]() x+2,解得x = 4
x+2,解得x = 4
∴点A、C的坐标分别为(0,2)、(4,0),
把A(0,2)、C(4,0)代入
解得![]() ,
,![]()
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)y=﹣![]() x2+
x2+![]() x+2
x+2![]()
∴抛物线的顶点D的坐标为![]() ,
,
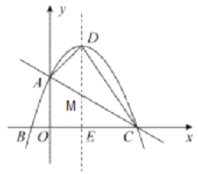
如图1,设直线AC与抛物线的对称轴交于点M
直线y=﹣![]() x+2中,当x =
x+2中,当x = ![]() 时,y =
时,y =![]()
点M的坐标为![]() ,则DM=
,则DM=![]()
∴△DAC的面积为=![]()
![]() ;
;
(3)当P到x轴的距离为4时,则
①当y=4时,﹣![]() x2+
x2+![]() x+2=4,
x+2=4,
而![]() ,所以方程没有实数根
,所以方程没有实数根
②当y= - 4时,﹣![]() x2+
x2+![]() x+2= - 4,
x+2= - 4,
解得![]()
则点P的坐标为![]() 或
或![]() ;
;
综上,存在一点P![]() 或
或![]() ,使它到x轴的距离为4.
,使它到x轴的距离为4.

练习册系列答案
相关题目