题目内容
【题目】作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
(1)将△ABC向右平移5个单位得到△A′B′C′;
(2)将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;
(3)连结EC′,则△A′EC′是 三角形.

【答案】(1)见解析;(2)见解析;(3)△A′EC′是等腰直角三角形
【解析】
(1)利用网格特点和平移的性质化出A、B、C的对应点A′、B′、C′,再连接点A′、B′、C′即可.
(2)利用网格特点和旋转的性质画出B′、C′的对应点D、E,再连接A′、D、E′即可;
(3)利用旋转的性质可判断△A′EC′是等腰直角三角形.
(1)如图,将A、B、C三点向右平移5个单位,得到A′、B′、C′,连接A′、B′、C′,△A′B′C′为所作;
(2)如图,将△A′B′C′绕点A′顺时针旋转90°得到△A′DE,△A′DE为所作;
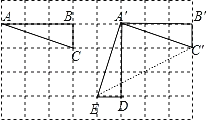
(3)连结EC′,如图,
∵△A′B′C′绕点A′顺时针旋转90°得到△A′DE,
∴A′E=A′C′,∠EA′C′=90°,
∴△A′EC′是等腰直角三角形.
故答案为:等腰直角

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目