题目内容
【题目】如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（ ）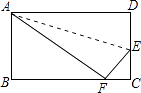
A.12
B.16
C.18
D.24
【答案】A
【解析】解：∵四边形ABCD为矩形，
∴AD=BC=10，AB=CD=8，
∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，
∴AF=AD=10，EF=DE，
在Rt△ABF中，
∵BF= 
=6，
∴CF=BC﹣BF=10﹣6=4，
∴△CEF的周长为：CE+EF+CF=CE+DE+CF=CD+CF=8+4=12．
所以答案是：A．
【考点精析】掌握勾股定理的概念和矩形的性质是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；矩形的四个角都是直角，矩形的对角线相等．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某天，一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg，然后在市场上按零售价出售，西红柿和豆角当天的批发价和零售价如下表所示：
品名 | 西红柿 | 豆角 |
批发价（单位：元/kg） | 2.0 | 1.5 |
零售价（单位：元/kg） | 2.9 | 2.6 |
如果西红柿和豆角全部以零售价售出，他当天卖这些西红柿和豆角赚了多少元钱？
