题目内容
【题目】我们给出如下定义:有一组相邻内角相等的凸四边形叫做“等邻角四边形”.请解答下列问题:
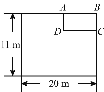
(1)“梯形、长方形、正方形”中“等邻角四边形”是____________;
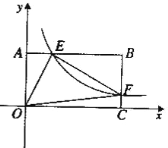
(2)如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是“等邻角四边形”;
是“等邻角四边形”;
(3)已知:在“等邻角四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,请画出相应图形,并直接写出
,请画出相应图形,并直接写出![]() 的长.
的长.

【答案】(1)长方形,正方形;(2)证明见详解;(3)CD的长为11或![]() 或2或10+
或2或10+![]() .
.
【解析】
(1)长方形和正方形至少有一组邻角相等,根据等邻角四边形的定义即可判断;
(2)取AC的中点为H,连接FH,EH,由三角形中位线可得EH∥AB,且EH= ![]() AB;FH∥CD,且FH=
AB;FH∥CD,且FH= ![]() CD,进而得到AB=CD,EH=FH,根据平行线性质可得∠2=∠4,∠1=∠3,进而得到∠4=∠3, 根据等角的补角相等可得∠AGE=∠GEC,进而得出结论;
CD,进而得到AB=CD,EH=FH,根据平行线性质可得∠2=∠4,∠1=∠3,进而得到∠4=∠3, 根据等角的补角相等可得∠AGE=∠GEC,进而得出结论;
(3)分四种情况:①∠D=∠A=90°时,② ∠A=∠B=90°时,③∠B=∠C=60°时,④∠C=∠D=60°时,分别画出四种情况的图形,作出辅助线,根据三角形的条件即可求得.
(1)长方形,正方形;
(2)如图所示,取AC中点为H连接FH,EH,
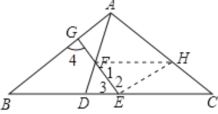
∵E为BC中点,
∴EH为![]() 的中位线,
的中位线,
∴EH∥AB,且EH= ![]() AB,
AB,
同理,FH∥CD,且FH= ![]() CD,
CD,
∵AB=AC,CD=AC,
∴AB=CD,EH=FH,
∴∠1=∠2,
∵EH∥AB,FH∥CD,
∴∠2=∠4,∠1=∠3,
∴∠4=∠3,
∵∠AGE+∠4=180°,∠GEC+∠3=180°,
∴∠AGE=∠GEC,
∴四边形AGEC是等邻角四边形;
(3)①当∠D=∠A=90°时,
如图所示,作BE⊥CD于E,
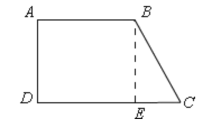
∵∠A=∠D=∠BED=90°,
∴四边形ADEB为矩形,
∴DE=AB=6,
在![]() 中,BC=10,∠C=60°,
中,BC=10,∠C=60°,
∴CE=5,
∴CD=DE+CE=11;
②当∠A=∠B=90°时,
如图所示,作CE⊥AD交AD的延长线于E,
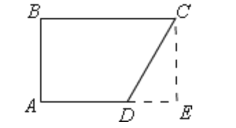
∵∠A=∠B=∠E,
∴四边形AECB为矩形,
∴AE=BC=10,CE=AB=6,
在![]() 中,∠DCE=∠BCE-∠BCD=30°,
中,∠DCE=∠BCE-∠BCD=30°,
设DE=x,则CD=2x,由勾股定理得:
![]()
解得:![]()
∴CD= ![]() ;
;
③当∠B=∠C=60°时,
如图所示,分别延长AD,BC交于点E,
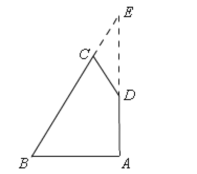
在![]() 中,∠B=60°,AB=6,
中,∠B=60°,AB=6,
∴BE=2AB=12, ∠E=30°,
∴CE=BE-BC=12-10=2,
∵∠BCD=60°,
∴∠CDE=∠CED=30°,
∴CD=CE=2,
④当∠C=∠D=60°时,
如图,分别延长DA,CB交于点E,
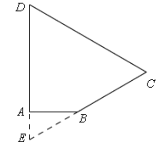
∵∠C=∠D=60°,
∴∠E=60°,CD=CE,
在![]() 中,∠E=60°,AB=6,
中,∠E=60°,AB=6,
设AE=x,则BE=2x,由勾股定理得:
![]()
解得:![]()
∴BE=![]() ,
,
∴CD=BC+BE=10+![]() ;
;
∴综上所述,CD的长为11或![]() 或2或10+
或2或10+![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:

根据上表解答下列问题:
(1)完成下表:
姓名 | 极差(分) | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 40 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.