��Ŀ����
����Ŀ��ijУҪ��С����С������ͬѧ����ѡһ�˲μ�ȫ����ѧ����������������ѡ�β����У������ijɼ��ֱ����±���

�����ϱ�����������⣺
��1������±���
���� | ����֣� | ƽ���ɼ����֣� | ��λ�����֣� | �������֣� | ���� |
�� | 40 | 80 | 75 | 75 | 190 |
�� |
��2��������β����У��ɼ��Ƚ��ȶ���ͬѧ��˭������80�����ϣ���80�֣��ijɼ���Ϊ���㣬��С����С��������β����е������ʸ��Ƕ��٣�
��3����������������ɼ��ﵽ80�����ϣ���80�֣��ͺܿ��ܻ��ɼ��ﵽ90�����ϣ���90�֣��ͺܿ��ܻ��һ�Ƚ�����ô����ΪӦѡ˭�μӱ����ȽϺ��ʣ�˵���������.
���𰸡���1������������2���ɼ��Ƚ��ȶ�����С�С����������Ϊ40%��С���������Ϊ80%����3��������.
��������
��1������ƽ��������λ�����������������ĸ��������ص�����
��2�����ӳ���ݵ���ɢ�̶������Է���ԽСԽ�ȶ���Ӧ��С��ijɼ��ȶ���С����������=![]() ��С���������=
�����������=![]() ��
��
��3��ѡ˭�μӱ����Ĵ𰸲�Ψһ��С��ijɼ��ȶ������Իļ��ʴ���С����90�����ϵijɼ�������С����һ�Ƚ��Ļ������
��1��С���ƽ����=![]() =80����λ��=80������=80������=
=80����λ��=80������=80������=![]() =40������=����������С����=90��70=20��
=40������=��������������=90��70=20��
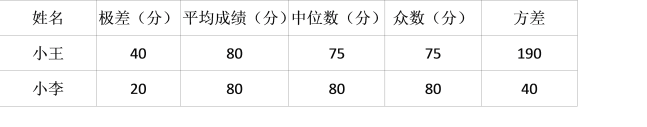
��2��������ο��������ɼ��Ƚ��ȶ�����С����С����������=![]() ��100%=40%��С���������=
��100%=40%�����������=![]() ��100%=80%��
��100%=80%��
��3������һ����ѡС��ȥ�μӱ�������ΪС��������ʸ�����4�ε�80�����ɼ��Ƚ��ȶ����������
����������ѡС��ȥ�μӱ�������ΪС���ijɼ����һ�Ƚ��Ļ��ʽϸ�����2��90�����ϣ���90�֣�������п��ܻ��һ�Ƚ���
��ע���𰸲�Ψһ����������ѡ����һ����ֻҪ�����������������֣���ѡ���˶�ȥ�μ����������ⲻ���֣���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ�˴ٽ����ܼ��ţ�������Լ�õ磬ij�н�ʵ�о��������õ���ݵ�۷�����ͼ�����߷�ӳ��ÿ��ÿ���õ���y��Ԫ�����õ���x���ȣ���ĺ�����ϵʽ��
��1������ͼ���ݵ�۷�����Ϊ�������Σ���д�±���
���� | ��һ�� | �ڶ��� | ������ |
ÿ���õ���x���ȣ� | 0��x��140 |
��2��С����ij���õ�120�ȣ��轻��� Ԫ
��3����ڶ���ÿ�µ��y��Ԫ�����õ���x���ȣ�֮��ĺ�����ϵʽ��
��4����ÿ���õ�������230��ʱ��ÿ����1�ȵ�Ҫ�ȵڶ����ึ���mԪ��С�ռ�ij���õ�290�ȣ������153Ԫ����m��ֵ��