题目内容
【题目】如图,P是矩形ABCD内部的一定点,M是AB边上一动点,连接MP并延长与矩形ABCD的一边交于点N,连接AN.已知AB=6cm,设A,M两点间的距离为xcm,M,N两点间的距离为y1cm,A,N两点间的距离为y2cm.小欣根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小欣的探究过程,请补充完整;
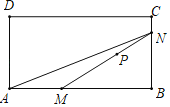
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 |
| 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐标系xOy中,描出以补全后的表中各组对应值所对应的点(x,y1),并画出函数y1的图象;
(3)结合函数图象,解决问题:当△AMN为等腰三角形时,AM的长度约为 cm.
【答案】(1) 4.80 ;(2)详见解析;(3) 3.3或4.8或5.7.
【解析】
(1)根据实际取点、画图、测量,即可解决问题;
(2)利用描点法画出函数图象即可解决问题;
(3)通过图象求出直线y=x与两个函数图象的交点坐标以及函数y1与y2的交点坐标即可解决问题.
(1)根据实际取点、画图、测量,可知当AM=2cm时,y1约为4.80cm.,
故答案为4.80.
(2)两个函数图象如图所示:
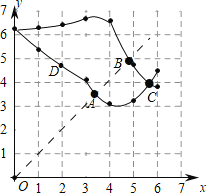
(3)两个函数与直线y=x的交点为A,B,函数y1与y2的交点为C,
观察图象可知:A(3.3,3.3),B(4.8,4.8),C(5.7,4).
∴△AMN为等腰三角形时,AM的值约为3.3或4.8或5.7.
故答案为3.3或4.8或5.7.

 步步高达标卷系列答案
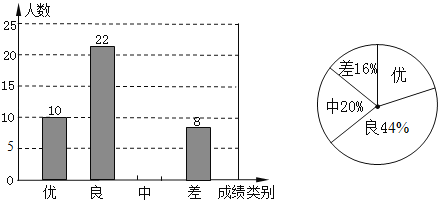
步步高达标卷系列答案【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
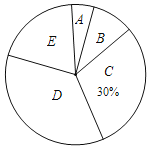
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.