Question

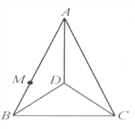
【题目】如图，BC是等腰三角形ABC与等腰三角形DBC的公共底边，AB=AC,BD=CD.

（1）求证：AD⊥BC.

（2）M是AB上的一点，在BC上是否存在一点P，使得PM+PD最小？若存在，请通过作图确定点P的位置；若不存在，请说明理由.

Answer 1

【答案】见解析

【解析】【试题分析】（1）考查线段中垂线的判定定理，AB=AC,得出点A在BC的中垂线上，同理，点D也在BC的中垂线上，由于两点确定一条直线，则AD⊥BC.

（2）属于小马饮水的问题，以BC为对称轴，作点D或M的对称点，D′或M′，连接D′M或M′D，交BC于点P，点P即是所求点. 图形见解析。

【试题解析】

证明：(1)

∵AB=AC,DB=DC,AD=AD，

∴△ABD≌△ACD，

∴∠BAD=∠CAD，

延长AD交BC于E,则

△ABE≌△ACE(SAS)，

∴∠AEB=∠AEC，

∵∠AEB+∠AEC=180°，

∴∠AEB=∠AEC=90°，

∴AD⊥BC.

(2)存在.

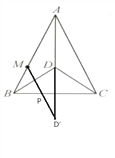
以BC为对称轴，作点D或M的对称点，D′或M′，连接D′M或M′D，交BC于点P，点P即是所求点.如图：