题目内容
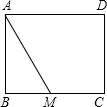如图，已知矩形ABCD，AB=2，BC=3，MB=MC，则sin∠AMB=分析：易得BM长，利用勾股定理可得AM长，则sin∠AMB等于AB与AM之比；
作DE⊥AM于点E，可得△AED∽△MBA，利用相似三角形的性质可得DE的长度．
作DE⊥AM于点E，可得△AED∽△MBA，利用相似三角形的性质可得DE的长度．
解答：解：易知BM=1.5，
∴AM=
=
，
∴sin∠AMB=2：
=
；
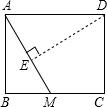
作DE⊥AM于点E，
易得△AED∽△MBA．
∴DE：AB=AD：AM，
∴DE=2.4．
∴AM=
| AB2+BM2 |
| 5 |
| 2 |
∴sin∠AMB=2：
| 5 |
| 2 |
| 4 |
| 5 |
作DE⊥AM于点E，
易得△AED∽△MBA．
∴DE：AB=AD：AM，
∴DE=2.4．
点评：考查了三角函数定义；相似三角形的对应边成比例的性质．
练习册系列答案
相关题目
如图，已知矩形DEFG内接于Rt△ABC，D在AB上，E、F在BC上，G在AC上，∠BAC=90°，AB=6cm，AC=8cm，
m/秒的速度移动，如果M、N两点同时出发，移动的时间为x秒（0≤x≤6）．
点A运动．
（2012•宁德质检）如图，已知Rt△ABC，∠B=90°，AB=8，BC=6，把斜边AC平均分成n段，以每段为对角线作边与AB、BC平行的小矩形，则这些小矩形的面积和是（ ）
如图，已知矩形ABCD中AB：BC=3：1，点A、B在x轴上，直线y=mx+n（0＜m＜n＜