��Ŀ����
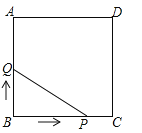
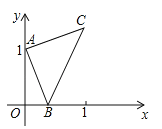
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
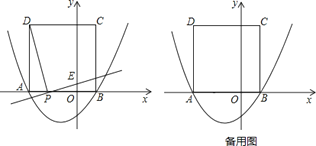
��1����ֱ��д����D�����꣺�� ����
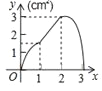
��2������P���߶�AO����P����A��O�غϣ����˶����δ�ʱ���߶�OE�ij������ֵ�����������ֵ��
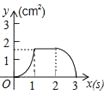
��3���Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
���𰸡�(1) ��-3��4����(2) PΪAO�е�ʱ��OE�����ֵΪ![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��![]() .
.
��������
��1������A�����������κ����Ľ���ʽ��������ʽ��Ȼ����õ�B�����꼴�����������ABCD�ı߳����Ӷ���õ�D�������꣮
��2��PA=t��OE=m��������DAP�ס�POE�õ�����ʽ���Ӷ��õ��й����������Ķ��κ���������ֵ���ɣ�
��3���ֵ�Pλ��y�������Ҳ�����������ۼ��ɵõ��ص����ֵ������
�⣺��1����A�����������κ����Ľ���ʽ
�ɵã�![]()
��ã�b=1��
�ʶ��κ����Ľ���ʽΪ��![]() ,
,
�ɵ�B������Ϊ����1��0����
��AB������4��
���������ε����ʿ�֪��AD=AB=4��
�ʵ�D����Ϊ��-3��4����
��2����PA=t��OE=m��
����DAP=��POE=��DPE=90������DAP�ס�POE��
��![]() ��
��
��![]() ��
��
����t=![]() ʱ��m�����ֵ
ʱ��m�����ֵ![]() ����PΪAO�е�ʱ��OE�����ֵΪ
����PΪAO�е�ʱ��OE�����ֵΪ![]() ��
��
��3�����ڣ�
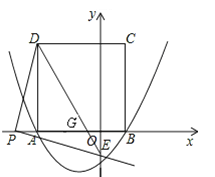
����P��y�����ʱ��P�������Ϊ����4��0����
����PAD�ס�OEG��OE=PA=1����OP=OA+PA=4��
�ߡ�ADG�ס�OEG����AG��GO=AD��OE=4��1��
��![]() ��
��
���ص����ֵ����=S��PAG![]() ��
��
����P����y���Ҳ�ʱ��P�������Ϊ��4��0����
�������裬��ʱ�ص����ֵ����Ϊ![]() ��
��

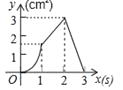
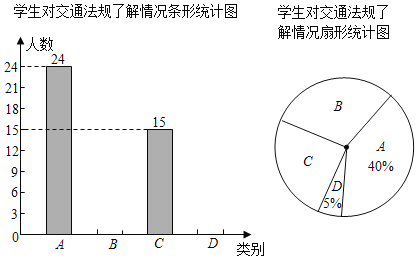
����Ŀ��ij��˾����![]() �������ţ�����ÿ�����ŵ�Ա����������Ӧÿ����������������Ƴ����µ�ͳ�Ʊ�������ͼ��
�������ţ�����ÿ�����ŵ�Ա����������Ӧÿ����������������Ƴ����µ�ͳ�Ʊ�������ͼ��

������������ÿ������������ͳ�Ʊ�
���� | Ա������ | ÿ��������������/��Ԫ |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
��1����������ͼ�У�C��������Ӧ��Բ�ĽǵĶ���Ϊ___________��
����ͳ�Ʊ��У�![]() ___________��
___________��![]() ___________��
___________��
��2���������˾ƽ��ÿ������������