题目内容
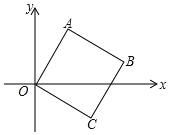
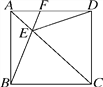
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
【答案】(1)见解析;(2)105°
【解析】试题分析:(1)根据正方形的性质可得BC=CD,∠ECB=∠ECD=45°,利用全等三角形的判定方法判定△BEC≌△DEC,(2)根据全等三角形的性质可得∠BEC=∠DEC= ![]() ,因为∠BED=120°,所以∠BEC=60°=∠AEF,
,因为∠BED=120°,所以∠BEC=60°=∠AEF,
所以∠EFD=60°+45°=105°.
试题解析: (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°,
∴在△BEC与△DEC中,
 ,
,
∴△BEC≌△DEC(SAS),
(2)∵△BEC≌△DEC,
∴∠BEC=∠DEC= ![]() ,
,
∵∠BED=120°,
∴∠BEC=60°=∠AEF,
∴∠EFD=60°+45°=105°.

练习册系列答案
相关题目