题目内容
【题目】问题提出 平面内不在同一条直线上的三点确定一个面,那么平面内的四点(任意三点均不在同一直线上),能否在同一个面上呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
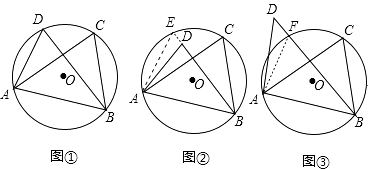
(1)当C、D在线段AB的同侧时. 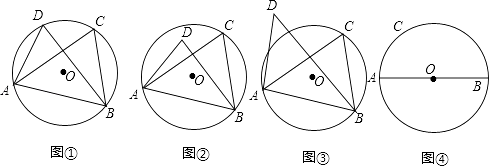
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 .
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB(填“=”、“>”、“<”)
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形. 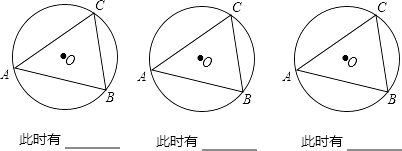
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
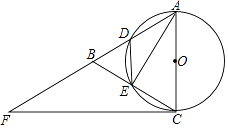
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线? 已知:如图,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB
作法:①连接CA、CB
②在CB上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB与M;
⑤连接D、M并延长,交⊙O于N,连接CN,则CN⊥AB.
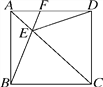
请安上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)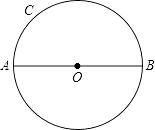
【答案】
(1)同弧所对的圆周角相等;<;>;当C、D在线段AB的同侧且∠ACB=∠ADB时,A、B、C、D四点在同一个圆上
(2)当C、D在线段AB的异侧且∠ACB+∠ADB=180°时,A、B、C、D四点在同一个圆上
(3)解:图⑦即为所求作.
∵AB是⊙0的直径,
∴∠ACB=∠ADB=90°,即BC⊥AF,AD⊥BF,
∴根据三角形的三条高交于同一点可得:FM⊥AB.
∴∠EMB=90°.
∴∠EMB+∠EDB=180°.
∴由(2)中的结论可得:点E、D、B、M在同一个圆上,如图⑦所示.
∴∠EMD=∠EBD.
∵∠CND=∠CBD,
∴∠CND=∠EMD.
∴CN∥EM.
∴∠CHB=∠EMB.
∵∠EMB=90°,
∴∠CHB=90°,即CN⊥AB.
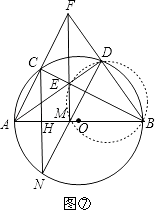
【解析】解:(1)①如图①,根据“同弧所对的圆周角相等”得∠ACB=∠ADB. ②如图②,延长BD交⊙O于点E,
∵∠AEB=∠ACB,∠AEB<∠ADB
∴∠ACB<∠ADB.
③如图③,连接AF,
∵∠AFB=∠ACB,∠AFB>∠ADB
∴∠ACB>∠ADB.
所以答案是:同弧所对的圆周角相等、<、>、
当C、D在线段AB的同侧且∠ACB=∠ADB时,A、B、C、D四点在同一个圆上.
2)①如图④,
∵ ![]() 与
与 ![]() 的度数之和等于360°,
的度数之和等于360°,
且∠ADB的度数等于 ![]() 度数的一半,
度数的一半,
∠ACB的度数等于 ![]() 度数的一半,
度数的一半,
∴∠ACB+∠ADB=180°.
②如图⑤,延长AD交⊙O于点E,连接BE,
∵∠ACB+∠AEB=180°,∠AEB<∠ADB,
∴∠ACB+∠ADB>180°.
③如图⑥,连接BF,
∵∠ACB+∠AFB=180°,∠AFB>∠ADB,
∴∠ACB+∠ADB<180°.
所以答案是:∠ACB+∠ADB=180°、∠ACB+∠ADB>180°、∠ACB+∠ADB<180°.
当C、D在线段AB的异侧且∠ACB+∠ADB=180°时,A、B、C、D四点在同一个圆上.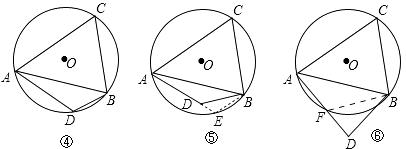
【考点精析】通过灵活运用平行线的判定与性质和三角形的外角,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.