题目内容
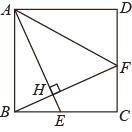
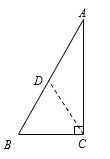
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.
【答案】见解析
【解析】
先在∠ACB的内部作∠BCD=∠B,CD与AB相交于点D.根据等腰三角形的性质得到DC=DB,再根据三角形的内角和定理得到∠B+∠ACD=90°,根据题意得到DA=DB=DC,最终得到CD=![]() AB.
AB.
在∠ACB的内部作∠BCD=∠B,
CD与AB相交于点D.
∵∠BCD=∠B,
∴DC=DB,
∵∠BCD+∠ACD=90°,
∴∠B+∠ACD=90°.
又∵∠A+∠B=90°,
∴∠ACD=∠A.
∴DA=DC.
∴DA=DB=DC,
即CD是斜边AB上的中线,且CD=![]() AB.
AB.

练习册系列答案
相关题目