题目内容
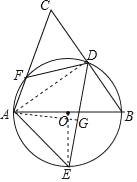
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)求证:∠E=∠C;
(2)若DF=6cm,cosB=![]() ,E是弧AB的中点,求DE的长.
,E是弧AB的中点,求DE的长.
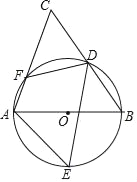
【答案】(1)证明见解析;(2)DE= 14![]() .
.
【解析】分析:(1)直接利用圆周角定理得出AD⊥BC,再利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;
(2)根据cosB=![]() ,得出AB的长,即可求出AE的长,解直角三角形即可得到结论.
,得出AB的长,即可求出AE的长,解直角三角形即可得到结论.
详解:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=12,
∵cosB=![]() ,
,
∴AB=20,
∵E是![]() 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=10,
∴AE=10![]() ,
,
∵E是![]() 的中点,
的中点,
∴∠ADE=∠BDE=45°,
∴DG=AG=ADsin45°=16×![]() =8
=8![]() ,EG=
,EG=![]() =6
=6![]() ,
,
∴DE=DG+GE=14![]() .
.

练习册系列答案
相关题目