Question

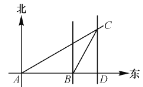
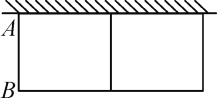
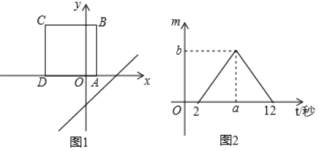
【题目】如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（ ）

A. 5B. 4C. 3D. 2

Answer 1

【答案】A

【解析】

根据题意可分析出当t=2时，l经过点A，从而求出OA的长，l经过点C时，t=12，从而可求出a，由a的值可求出AD的长，再根据等腰直角三角形的性质可求出BD的长，即b的值.

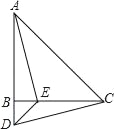
解：连接BD,如图所示：

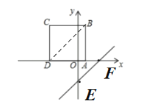
直线y＝x﹣3中，令y＝0，得x＝3；令x＝0，得y＝﹣3，

即直线y＝x﹣3与坐标轴围成的△OEF为等腰直角三角形，

∴直线l与直线BD平行，即直线l沿x轴的负方向平移时，同时经过B，D两点，

由图2可得，t＝2时，直线l经过点A，

∴AO＝3﹣2×1＝1，

∴A（1，0），

由图2可得，t＝12时，直线l经过点C，

∴当t＝+2＝7时，直线l经过B，D两点，

∴AD＝（7﹣2）×1＝5，

∴在等腰Rt△ABD中，BD＝，

即当a＝7时，b＝．

故选：A．