题目内容
换元法是一种将复杂问题变得简单的一种方法,其主要的思想是,把某个式子看成一个整体,用一个变量去代替它.如:
解方程:x4-2x2-8=0
解:令t=x2,则t≥0原方程可化为:t2-2t-8=0
解得:t1=4,t2=-2
因为t2=-2<0和t≥0不相符,∴t1=4,即x2=4,∴x1=2,x2=-2
请认真阅读上述题目,并解方程:(
)4+(
)2=2.
解方程:x4-2x2-8=0
解:令t=x2,则t≥0原方程可化为:t2-2t-8=0
解得:t1=4,t2=-2
因为t2=-2<0和t≥0不相符,∴t1=4,即x2=4,∴x1=2,x2=-2
请认真阅读上述题目,并解方程:(
| 2x-1 |
| x |
| 2x-1 |
| x |
分析:先设(
)2=t,则方程即可变形为t2+t-2=0,解方程即可求得t即(
)2的值.
| 2x-1 |
| x |
| 2x-1 |
| x |
解答:解:设(
)2=t(t≥0),则方程即可变形为t2+t-2=0,即(t-1)(t+2)=0,
解得t=1或t=-2(不合题意,舍去).
所以(
)2=1,
开平方,得
=±1,即2x-1=±x,
解得,x=1或x=
.
经检验,x=1或x=
都是原方程的解,
所以,原方程的根是:x=1或x=
.
| 2x-1 |
| x |
解得t=1或t=-2(不合题意,舍去).
所以(
| 2x-1 |
| x |
开平方,得
| 2x-1 |
| x |
解得,x=1或x=
| 1 |
| 3 |
经检验,x=1或x=
| 1 |
| 3 |
所以,原方程的根是:x=1或x=
| 1 |
| 3 |
点评:本题主要考查了换元法解一元二次方程,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
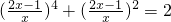 .
.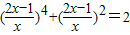 .
. 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.