题目内容
换元法是把一个比较复杂的数学式子的一部分看成是一个整体,用另一个字母代替这一部分(即换元).换元法的好处是能使式子得到简化,各项的关系容易看清,便于解决问题.此方法充分体现了整体的数学思想.例如:用换元法解分式方程| 2x-1 |
| x |
| x |
| 2x-1 |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 12 |
| x2-2x |
分析:本题先设x2-2x为y,则原方程可化为y2+y-12=0,解出y的值,最后反代入解出x的值.
解答:解:设x2-2x为y,则原方程可化为y2+y-12=0,
解得y1=-4y2=3,
∴有①x2-2x=-4 ②x2-2x=3,
∴①无实数根,②解得x1=-1,x2=3,
经检验,x1=-1,x2=3是原方程的解.
解得y1=-4y2=3,
∴有①x2-2x=-4 ②x2-2x=3,
∴①无实数根,②解得x1=-1,x2=3,
经检验,x1=-1,x2=3是原方程的解.
点评:本题主要考查用换元法解分式方程,关键是先进行适当换元再利用反代法求解.

练习册系列答案
相关题目
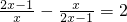 时,如果设
时,如果设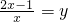 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成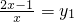 和
和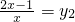 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: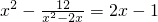 .
. 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.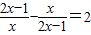 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.