题目内容
【题目】如图1，已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一条直线，且B、C在A、E的异侧，BD⊥AE于D，CE⊥AE于E．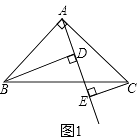
（1）求证：BD=DE+CE；
（2）若直线AE绕A点旋转到图2位置时（BD＜CE），其余条件不变，则BD与DE、CE的数量关系如何？请予以证明；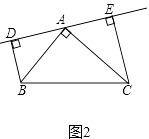
（3）若直线AE绕A点旋转到图3位置时（BD＞CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果，不需说明理由；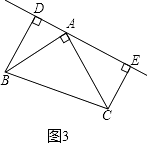
（4）根据以上的讨论，请用简洁的语言表述BD与DE、CE的数量关系．
【答案】
（1）
证明：∵∠BAC=90°，
∴∠BAD+∠EAC=90°，
又∵BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∠BAD+∠ABD=90°，
∴∠ABD=∠EAC，
在△ABD与△CAE中，
，
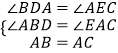∴△ABD≌△CAE，
∴BD=AE，AD=CE，
∵AE=AD+DE=CE+DE，
∴BD=DE+CE
（2）
证明：∵∠BAC=90°，
∴∠BAD+∠EAC=90°，
又∵BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∠BAD+∠ABD=90°，
∴∠ABD=∠EAC，
在△ABD与△CAE中，
，
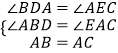∴△ABD≌△CAE，
∴BD=AE，AD=CE，
∵DE=AD+AE=CE+BD，
∴DE=BD+CE
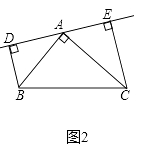
（3）
证明：∵∠BAC=90°，
∴∠BAD+∠EAC=90°，
又∵BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∠BAD+∠ABD=90°，
∴∠ABD=∠EAC，
在△ABD与△CAE中，
，
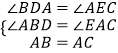∴△ABD≌△CAE，
∴BD=AE，AD=CE，
∵DE=AD+AE=BD+CE，
∴DE=BD+CE
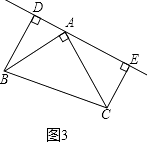
（4）
证明：BD与CE的和等于DE或BD等于DE与CE的和
【解析】（1）证明△ABD≌△CAE，即可证得BD=AE，AD=CE，而AE=AD+DE=CE+DE，即可证得；（2）（3）图形变换了，但是（1）中的全等关系并没有改变，因而BD与DE、CE的关系并没有改变；（4）把BD与DE、CE的关系用语言表述出来即可．
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．
