Question

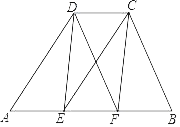
【题目】如图，等腰三角形ABC中，AB=AC=5cm，BC=8cm，动点N从点C出发，沿线段CB以2cm/s的速度向点B运动，并在达到点B后，立即以同样的速度返回向点C运动；同时动点M从点B出发，沿折线B﹣A﹣C以1cm/s的速度向点C运动，当点N回到点C时，两个动点同时停止运动．⊙M是以M为圆心，1cm为半径的圆，设运动时间为t（s） （t＞0）

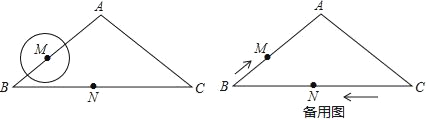
（1）tanB=　 　；

（2）当点M在线段AB上运动，且⊙M与BC相切时，求t的值；

（3）当t为何值时，⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧，且经过交点和点N的直线与⊙M相切？

Answer 1

【答案】（1）；（2）t=；（3）满足条件的t的值为s或s或s．

【解析】试题分析：（1）作AH⊥BC用H，根据等腰三角形的性质以及勾股定理分别求得BH、AH的长，再利用正切的定义即可求得；

（2）作MK⊥BC于K，根据⊙M与BC相切，则可得MK=1，再根据sinB=，即可得；

（3）分0＜t≤4， 4＜t≤8，进行讨论即可得

试题解析：（1）如图1中，作AH⊥BC用H．

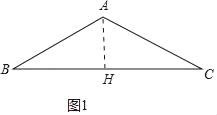
∵AB=AC=5，AH⊥BC，

∴BH=CH=BC=4，AH==3，

∴tanB=，

故答案为： ；

（2）如图2中，作MK⊥BC于K，

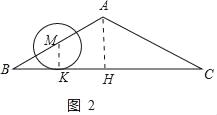
∵⊙M与BC相切，

∴MK=1，

∵sinB=，

∴BM=，

∴t=s时，⊙M与BC相切；

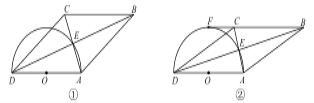
（3）如图设⊙M交AB于P、G，连接GN，

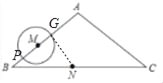
①当0＜t≤4时，如果NG是⊙M的切线，则GN⊥AB，则有cosB=，

∴，

解得：t=，

②当PN是切线时，同法可得， ，

解得t=．

③当4＜t≤8时，同法可得， 或，

解得t=3（不合题意舍弃）或t=，

综上所述，满足条件的t的值为s或s或s．